
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

【答案】(1)30°;(2)8.
【解析】
(1)由在△ABC中,AB=AC,∠A=40°,利用等腰三角形的性质,即可求得∠ABC的度数,然后由AB的垂直平分线MN交AC于点D,根据线段垂直平分线的性质,可求得AD=BD,继而求得∠ABD的度数,则可求得∠DBC的度数;
(2)根据AE=6,AB=AC,得出CD+AD=12,由△CBD的周长为20,代入即可求出答案.
(1)∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=∠C=70°,
∵AB的垂直平分线MN交AC于点D,
∴AD=BD,
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=30°;
(2)∵AE=6,
∴AC=AB=2AE=12,
∵△CBD的周长为20,
∴BC=20﹣(CD+BD)=20﹣(CD+AD)=20﹣12=8,
∴BC=8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到社会的广泛关注,某校政教处对部分学生就校园安全知识的了解程度,进行了随机抽样调查,并绘制了如下两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有______名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,
,![]() 、
、![]() 分别是
分别是![]() 轴、
轴、![]() 轴上的点.如果以点
轴上的点.如果以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,则
为顶点的四边形是平行四边形,则![]() 的坐标为__________.
的坐标为__________.
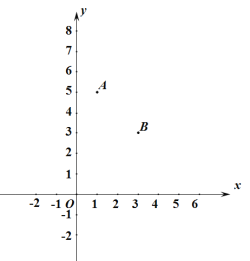
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,点E,F分别是线段BC,DC上的动点.当△AEF的周长最小时,则∠EAF的度数为( )

A. 90°B. 80°C. 70°D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
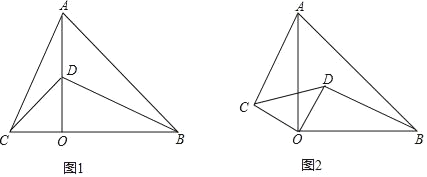
【题目】已知,△AOB,△COD是有公共顶点的两个等腰直角三角形,∠AOB=∠COD=90°,连接AC,BD.
(1)如果△AOB,△COD的位置如图1所示,点D在AO上,请判断AC与BD的数量关系,并说明理由;
(2)如果△AOB,△COD的位置如图2所示,请判断AC与BD的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
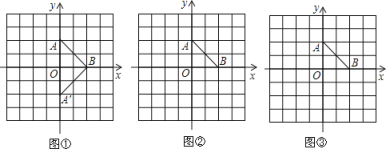
【题目】如图①,△A′OB是将等腰直角三角形AOB的顶点A经过一次变换后所得的等腰直角三角形,请在图②③中,保持O,B位置不动,对点A经过一次(或一组)变换,使变换后的△A′OB仍是等腰直角三角形.要求:作出△A′OB,并写出点A的变换方式.
方式1:把点A向下平移4个单位;
方式2:_________________;
方式3:_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(![]() ,0),AB⊥
,0),AB⊥![]() 轴,且AB=10,点C(0,b),
轴,且AB=10,点C(0,b),![]() ,b满足
,b满足![]() .点P(t,0)是线段AO上一点(不包含A,O)
.点P(t,0)是线段AO上一点(不包含A,O)
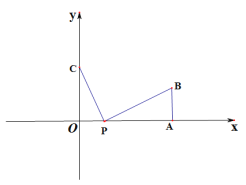
(1)当t=5时,求PB:PC的值;
(2)当PC+PB最小时,求t的值;
(3)请根据以上的启发,解决如下问题:正数m,n满足m+n=10,且正数![]() =
=![]() ,则正数
,则正数![]() 的最小值=________.
的最小值=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)= ![]() . 例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)=
. 例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)= ![]() .
.
(Ⅰ)如果一个正整数m是另外一个正整数n的平方,我们称正整数m是完全平方数.
求证:对任意一个完全平方数m,总有F(m)=1;
(Ⅱ)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数t为“吉祥数”,求所有“吉祥数”;
(Ⅲ)在(2)所得“吉祥数”中,求F(t)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com