
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1 , 交x轴正半轴于点O2 , 以O2为圆心,O2O为半径画圆,交直线l于点P2 , 交x轴正半轴于点O3 , 以O3为圆心,O3O为半径画圆,交直线l于点P3 , 交x轴正半轴于点O4;…按此做法进行下去,其中 ![]() 的长为 .
的长为 . 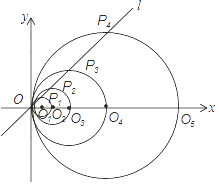
【答案】22015π
【解析】解:连接P1O1 , P2O2 , P3O3…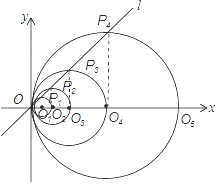
∵P1 是⊙O2上的点,
∴P1O1=OO1 ,
∵直线l解析式为y=x,
∴∠P1OO1=45°,
∴△P1OO1为等腰直角三角形,即P1O1⊥x轴,
同理,PnOn垂直于x轴,
∴ ![]() 为
为 ![]() 圆的周长,
圆的周长,
∵以O1为圆心,O1O为半径画圆,交x轴正半轴于点O2 , 以O2为圆心,O2O为半径画圆,交x轴正半轴于点O3 , 以此类推,
∴OOn=2n﹣1 ,
∴ ![]() =
= ![]() 2πOOn=
2πOOn= ![]() π2n﹣1=2n﹣2π,
π2n﹣1=2n﹣2π,
当n=2017时, ![]() =22015π.
=22015π.
故答案为 22015π.
由题意可作辅助线,连接P1O1 , P2O2 , P3O3…,根据直线l解析式为y=x可得∠P1OO1=45°,即△P1OO1为等腰直角三角形,所以有P1O1⊥x轴,同理可得PnOn垂直于x轴,弧P n On + 1的长=圆周长![]()
![]() ,所以OOn=
,所以OOn=![]() ,则弧PnOn+1=
,则弧PnOn+1=![]()
![]() 2
2![]()
![]()
![]() ,把n=2017代入计算即可求解。
,把n=2017代入计算即可求解。


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】“校园安全”受到社会的广泛关注,某校政教处对部分学生就校园安全知识的了解程度,进行了随机抽样调查,并绘制了如下两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有______名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△A′OB是将等腰直角三角形AOB的顶点A经过一次变换后所得的等腰直角三角形,请在图②③中,保持O,B位置不动,对点A经过一次(或一组)变换,使变换后的△A′OB仍是等腰直角三角形.要求:作出△A′OB,并写出点A的变换方式.
方式1:把点A向下平移4个单位;
方式2:_________________;
方式3:_________________.
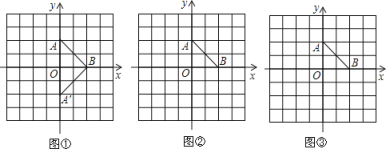
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(![]() ,0),AB⊥
,0),AB⊥![]() 轴,且AB=10,点C(0,b),
轴,且AB=10,点C(0,b),![]() ,b满足
,b满足![]() .点P(t,0)是线段AO上一点(不包含A,O)
.点P(t,0)是线段AO上一点(不包含A,O)
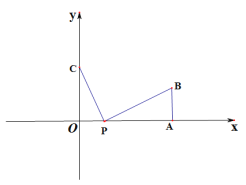
(1)当t=5时,求PB:PC的值;
(2)当PC+PB最小时,求t的值;
(3)请根据以上的启发,解决如下问题:正数m,n满足m+n=10,且正数![]() =
=![]() ,则正数
,则正数![]() 的最小值=________.
的最小值=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8 …,顶点依次为A1,A2,A3,A4,A5,…,则顶点A55的坐标是( )
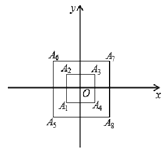
A. (13,13) B. (-13,-13) C. (-14,-14) D. (14,14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离( )cm.

A.14B.15C.16D.17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队承包一项工程,如果甲工程队单独施工,恰好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则恰好如期完成.
(1)问原来规定修好这条公路需多少长时间?
(2)现要求甲、乙两个工程队都参加这项工程,但由于受到施工场地条件限制,甲、乙两工程队不能同时施工.已知甲工程队每月的施工费用为4万元,乙工程队每月的施工费用为2万元.为了结算方便,要求:甲、乙的施工时间为整数个月,不超过15个月完成.当施工费用最低时,甲、乙各施工了多少个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)= ![]() . 例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)=
. 例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)= ![]() .
.
(Ⅰ)如果一个正整数m是另外一个正整数n的平方,我们称正整数m是完全平方数.
求证:对任意一个完全平方数m,总有F(m)=1;
(Ⅱ)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数t为“吉祥数”,求所有“吉祥数”;
(Ⅲ)在(2)所得“吉祥数”中,求F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为[x].即当n为非负整数时,若n﹣ ![]() ≤x<n+
≤x<n+ ![]() ,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题:
,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题:
(1)填空:
①若[x]=3,则x应满足的条件:________;
②若[3x+1]=3,则x应满足的条件:________;
(2)求满足[x]= ![]() x﹣1的所有非负实数x的值.
x﹣1的所有非负实数x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com