
【题目】平面直角坐标系中,点A、B分别在x轴正半轴、y轴正半轴上,AO=BO,△ABO的面积为8.
(1)求点A的坐标;
(2)点C、D分别在x轴负半轴、y轴正半轴上(D在B点上方),AB⊥CD于E,设点D纵坐标为t,△BCE的面积为S,求S与t的函数关系;
(3)在(2)的条件下,点F为BE中点,连接OF交BC于G,当∠FOB+∠DAE=45°时,求点E坐标.


【答案】(1)A(4,0);(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用三角形的面积公式构建方程即可解决问题.
(2)证明△CEA和△COD是等腰直角三角形,由EN⊥AC,推出![]() ,AC=4+t,根据S=S△AEC-S△ABC计算即可.
,AC=4+t,根据S=S△AEC-S△ABC计算即可.
(3)过点F作FM⊥AC于点M,由(2)求出点F的坐标为![]() ,从而得到
,从而得到
![]() ,
,![]() ,由∠ABO=∠BDA+∠BAD=45°,∠FOB+∠DAE=45°,得出∠FOB=∠BDA,进而得出∠MFO=∠ODA,tan∠MFO =tan∠ODA,故而
,由∠ABO=∠BDA+∠BAD=45°,∠FOB+∠DAE=45°,得出∠FOB=∠BDA,进而得出∠MFO=∠ODA,tan∠MFO =tan∠ODA,故而![]() ,
,
即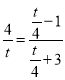 ,解出t的值,再求点E的坐标即可.
,解出t的值,再求点E的坐标即可.
(1)由题意可得:![]() ,
,
∴OA2=16,
∵OA>0,
∴OA=OB=4,
∴A(4,0),B(0,4).
(2)如图,过点E作EN⊥AC于点N.
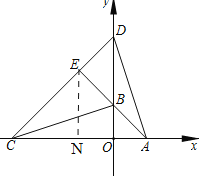
∵∠AOB=90°,OA=OB,
∴∠OAB=45°,
∵AB⊥CD,
∴∠CEA=90°,
∴∠ECA=45°,
∴△CEA是等腰直角三角形,
∵∠ECA=45°,∠COD=90°,
∴∠CDO=45°,
∴△CDO是等腰直角三角形.
∵点D纵坐标为t,
∴CO=DO=t.
∵OA=OB=4,
∴AC=t+4.
∴![]() ,
,
∴![]() ;
;
∴S与t的函数关系是:![]() .
.
(3)如图,过点F作FM⊥AC于点M,
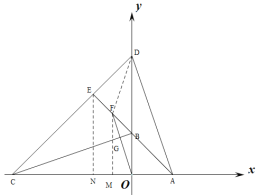
由(2)可知,![]() ,
,
∴![]() ,
,
∴点E的坐标为![]() ,
,
∵点B(0,4),点F为BE中点,
∴点F的坐标为![]() ,
,
∴![]() ,
,![]() ,
,
∵∠ABO=∠BDA+∠BAD=45°,∠FOB+∠DAE=45°,
∴∠FOB=∠BDA,
∴OF∥AD,
∵FM⊥AC,
∴FM∥DO,
∴∠MFO=∠ODA,
∴tan∠MFO =tan∠ODA,
∴![]() ,
,
即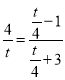 ,
,
解得t=12或4=-4(不合题意,舍去)
∴点E的坐标为![]() .
.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨l元,则每个月少卖l0件(每件售价不能高于65元).设每件商品的售价上x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量戈的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知等边三角形ABC和等边三角形DBC有公共边BC,以图中某个点为旋转中心,旋转△DBC使它和△ABC重合,则旋转中心可以是________.(写出一个旋转中心即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日世界读书日这天,滨江初二年级的学生会,就2018年寒假读课外书数量(单位:本)做了调查,他们随机调查了甲、乙两个班的10名同学,调查过程如下
收集数据
甲、乙两班被调查者读课外书数量(单位:本)统计如下:
甲:1,9,7,4,2,3,3,2,7,2
乙:2,6,6,3,1,6,5,2,5,4
整理、描述数据绘制统计表如下,请补全下表:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 4 | 3 | ||
乙 | 6 | 3.2 |
分析数据、推断结论
(1)该校初二乙班共有40名同学,你估计读6本书的同学大概有_____人;
(2)你认为哪个班同学寒假读书情况更好,写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扬州市教育行政部门为了了解八年级学生每学期参加综合实践活动的情况,随机调查了部分学生,并将他们一学期参加综合实践活动的天数进行统计,绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题:
(1)参加调查的八年级学生总人数为_______人;
(2)根据图中信息,补全条形统计图;扇形统计图中“活动时间为4天”的扇形所对应的圆心角的度数为_______;
(3)如果全市共有八年级学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
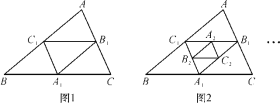
【题目】如图,在图1中,A1,B1,C1分别是△ABC的边BC,CA,AB的中点,在图2中,A2,B2,C2分别是△A1B1C1的边B1C1,C1A1,A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有___个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com