
【题目】如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是 . 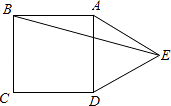
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 满足
满足![]() ,则称
,则称![]() 互为“相关抛物线”给出如下结论:
互为“相关抛物线”给出如下结论:
①y1与y2的开口方向,开口大小不一定相同; ②y1与y2的对称轴相同;③若y2的最值为m,则y1的最值为k2m;④若函数![]() 与x 轴的两交点间距离为d,则函数
与x 轴的两交点间距离为d,则函数![]() 与x 轴的两交点间距离也为
与x 轴的两交点间距离也为![]() .其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
.其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A,C分别在DG、DE上,连接AE、BG. 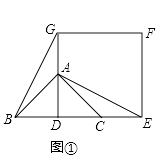
(1)试猜想线段BG和AE的数量关系,请直接写出你得到的结论;
(2)将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图②,(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由. 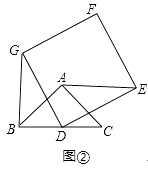
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com