
【题目】如图①,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A,C分别在DG、DE上,连接AE、BG. 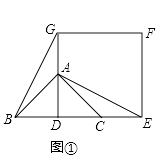
(1)试猜想线段BG和AE的数量关系,请直接写出你得到的结论;
(2)将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图②,(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由. 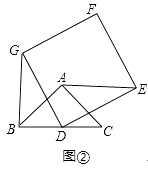
【答案】
(1)解:BG=AE.理由如下:
如图①,∵△ABC是等腰直角三角形,∠BAC=90°,
点D是BC的中点,
∴BD=CD=AD,
∵在△BDG和△ADE中, 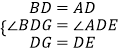 ,
,
∴△BDG≌△ADE(SAS),
∴BG=AE
(2)解:证明:连接AD,
∵Rt△BAC中,D为斜边BC的中点,
∴AD=BD,AD⊥BC,
∴∠ADG+∠GDB=90°,
∵EFGD为正方形,
∴DE=DG,且∠GDE=90°,
∴∠ADG+∠ADE=90°,
∴∠BDG=∠ADE,
在△BDG和△ADE中, 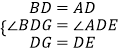 ,
,
∴△BDG≌△ADE(SAS),
∴BG=AE.
【解析】(1)在Rt△BDG与Rt△EDA;根据边角边定理易得Rt△BDG≌Rt△EDA;故BG=AE;(2)连接AD,根据直角三角形与正方形的性质可得Rt△BDG≌Rt△EDA;进而可得BG=AE.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】某地电话拨号入网有两种收费方式,用户可以任选其一:
(A)计时制:0.05元/分;
(B)包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为![]() 分,请你用含
分,请你用含![]() 的代数式分别写出两种收费方式下该用户应该支付的费用;
的代数式分别写出两种收费方式下该用户应该支付的费用;
(2)如果某用户一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.
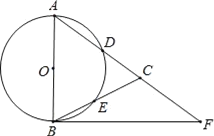
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个事件,事件A:367人中至少有2人生日相同;事件B:抛掷一枚均匀的骰子,朝上的面点数为偶数.下列说法正确的是( )
A.事件A、B都是随机事件
B.事件A、B都是必然事件
C.事件A是随机事件,事件B是必然事件
D.事件A是必然事件,事件B是随机事件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com