
【题目】如图,已知∠ADC=∠EFC,∠3=∠C,证明∠1=∠2的过程如下,请填上对应的理由.
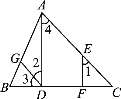
解:∵∠ADC=∠EFC(已知),
∴AD∥EF(___________________________________).
∴∠1=∠4(__________________________________).
又∵∠3=∠C(已知),
∴AC∥DG(__________________________________).
∴∠2=∠4(_________________________________).
∴∠1=∠2(________________________).
【答案】同位角相等,两直线平行;两直线平行,同位角相等;同位角相等,两直线平行;两直线平行,内错角相等;等量代换.
【解析】
由∠ADC=∠EFC,根据同位角相等,两直线平行,可判定AD∥EF,继而可得∠1=∠4,又由∠3=∠C,易判定AC∥DG,继而可得∠2=∠4,利用等量代换即可得∠1=∠2.
∵∠ADC=∠EFC(已知),
∴AD∥EF(同位角相等,两直线平行).
∴∠1=∠4(两直线平行,同位角相等).
又∵∠3=∠C(已知),
∴AC∥DG(同位角相等,两直线平行).
∴∠2=∠4(两直线平行,内错角相等).
∴∠1=∠2(等量代换),
故答案为:同位角相等,两直线平行;两直线平行,同位角相等;同位角相等,两直线平行;两直线平行,内错角相等;等量代换.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A, ![]() .则下列结论中不一定正确的是( )
.则下列结论中不一定正确的是( ) 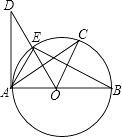
A.BA⊥DA
B.OC∥AE
C.∠COE=2∠CAE
D.OD⊥AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,
, ![]() 与
与![]() 互余,
互余, ![]() 平分
平分![]() .
.
(1)在图1中,若![]() ,则
,则![]() ______
______![]() ,
, ![]() ______
______![]() .
.
(2)在图1中,设![]() ,
, ![]() ,请探究
,请探究![]() 与
与![]() 之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);
之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);
(3)在已知条件不变的前提下,当![]() 绕着点O顺时针转动到如图2的位置,此时
绕着点O顺时针转动到如图2的位置,此时![]() 与
与![]() 之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时
之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时![]() 与
与![]() 之间的数量关系.
之间的数量关系.
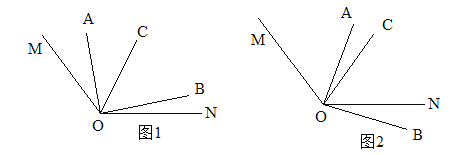
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,双曲线y= ![]() 与直线y=﹣2x+2交于点A(﹣1,a).
与直线y=﹣2x+2交于点A(﹣1,a).
(1)求a,m的值;
(2)求该双曲线与直线y=﹣2x+2另一个交点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B( ![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C. 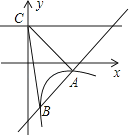
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下面图象表示小红从家里出发去散步过程中离家的距离s(米)与散步所用的时间t(分)之间的关系,请根据图象,确定下面描述符合小红散步情景的是( )
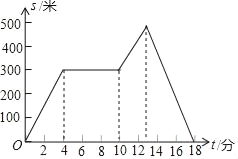
A. 从家出发,到了一个公共阅报栏,看了一会儿报,就回家了
B. 从家里出发,散了一会儿步,就找同学去了,18分钟后才开始返回
C. 从家里出发,一直散步(没有停留),然后回家了
D. 从家出发,到了一个公共阅报栏,看了一会儿报,继续向前走了一段后,然后回家了
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将△MCD平移至△NBA.
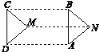
(1)图中平行且相等的线段有____________;
(2)图中相等的角有_______________ (写出三对即可);
(3)能够完全重合的三角形是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为6的正三角形纸片ABC按如下顺序进行两次折叠,展开后,得折痕AD、BE.(如图①),点O为其交点.如图②,若P、N分别为BE、BC上的动点.如图③,若点Q在线段BO上,BQ=1,则QN+NP+PD的最小值=_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com