
【题目】如图,在![]() 中,
中,![]() 的中垂线交
的中垂线交![]() 于点
于点![]() 交
交![]() 延长线于点
延长线于点![]() .若
.若![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 的面积是( )
的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我们做个折纸游戏:第一步:在一张矩形纸片的一端,利用图![]() 的方法折出一个正方形,然后把纸片展开;第二步:如图
的方法折出一个正方形,然后把纸片展开;第二步:如图![]() ,把这个正方形折成两个相等的矩形,再把纸片展开;第三步:折出内侧矩形的对角线
,把这个正方形折成两个相等的矩形,再把纸片展开;第三步:折出内侧矩形的对角线![]() ,并把它折到图
,并把它折到图![]() 中所示的
中所示的![]() 处;第四步:如图
处;第四步:如图![]() , 展平纸片,按照所得的
, 展平纸片,按照所得的![]() 点折出
点折出![]() .则矩形
.则矩形![]() 的宽
的宽![]() 与长
与长![]() 的比是__________.
的比是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读材料再回答问题.
对三个数x,y,z,规定![]() ;
;![]() 表示x,y,z这三个数中最小的数,如
表示x,y,z这三个数中最小的数,如![]() ,
,![]()
请用以上材料解决下列问题:
(1)若![]() ,求x的取值范围;
,求x的取值范围;
(2)①若![]() ,求x的值;
,求x的值;
②猜想:若![]() ,那么a,b,c大小关系如何?请直接写出结论;
,那么a,b,c大小关系如何?请直接写出结论;
③问:是否存在非负整数a,b,c使![]() 等式成立?若存在,请求出a,b,c的值;若不存在,请说明理由.
等式成立?若存在,请求出a,b,c的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清明节,除了扫墓踏青之外,传统时令小吃----青团也深受大家欢迎,知味观推出一款鲜花牛奶青团和一款芒果青团,鲜花牛奶青团每个售价是芒果青团的![]() 倍,4月份鲜花牛奶青团和芒果青团总计销售
倍,4月份鲜花牛奶青团和芒果青团总计销售![]() 个,鲜花牛奶青团销售额为
个,鲜花牛奶青团销售额为![]() 元,芒果青团销售额为
元,芒果青团销售额为![]() 元.
元.
(1)求鲜花牛奶青团和芒果青团的售价?
(2)5月份正值知味观店庆,决定再生产![]() 个青团回馈新老顾客,但考虑到芒果青团较受欢迎,同时也考虑受机器设备限制,因此芒果青团的个数不少于鲜花牛奶青团个数的
个青团回馈新老顾客,但考虑到芒果青团较受欢迎,同时也考虑受机器设备限制,因此芒果青团的个数不少于鲜花牛奶青团个数的![]() ,不多于鲜花牛奶青团的
,不多于鲜花牛奶青团的![]() 倍,其中,鲜花牛奶青团每个让利
倍,其中,鲜花牛奶青团每个让利![]() 元销售,芒果青团售价不变,并且让利后的鲜花牛奶青团售价不得低于芒果青团售价的
元销售,芒果青团售价不变,并且让利后的鲜花牛奶青团售价不得低于芒果青团售价的![]() ,问:知味观如何设计生产方案?使总销售额最大.
,问:知味观如何设计生产方案?使总销售额最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=32°,则下列结论错误的有( ) 
A.∠C′EF=32°
B.∠AEC=148°
C.∠BGE=64°
D.∠BFD=116°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A, ![]() .则下列结论中不一定正确的是( )
.则下列结论中不一定正确的是( ) 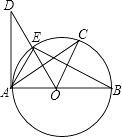
A.BA⊥DA
B.OC∥AE
C.∠COE=2∠CAE
D.OD⊥AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,双曲线y= ![]() 与直线y=﹣2x+2交于点A(﹣1,a).
与直线y=﹣2x+2交于点A(﹣1,a).
(1)求a,m的值;
(2)求该双曲线与直线y=﹣2x+2另一个交点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com