【题目】清明节，除了扫墓踏青之外，传统时令小吃----青团也深受大家欢迎，知味观推出一款鲜花牛奶青团和一款芒果青团，鲜花牛奶青团每个售价是芒果青团的倍，4月份鲜花牛奶青团和芒果青团总计销售个，鲜花牛奶青团销售额为元，芒果青团销售额为元．

（1）求鲜花牛奶青团和芒果青团的售价？

（2）5月份正值知味观店庆，决定再生产个青团回馈新老顾客，但考虑到芒果青团较受欢迎，同时也考虑受机器设备限制，因此芒果青团的个数不少于鲜花牛奶青团个数的，不多于鲜花牛奶青团的倍，其中，鲜花牛奶青团每个让利元销售，芒果青团售价不变，并且让利后的鲜花牛奶青团售价不得低于芒果青团售价的，问：知味观如何设计生产方案？使总销售额最大．

参考答案：

【答案】（1）芒果青团的售价为0.8元，则鲜花牛奶青团的售价为1元；（2）当0＜a≤0.2时，鲜花牛奶青团生产4800个，芒果青团生产7200个，销售额最大；当a=0.2时，销售额不变；当0.2＜a≤0.4时，鲜花牛奶青团生产4000个，芒果青团生产8000个，销售额最大．

【解析】

（1）设芒果青团的售价为x元，则鲜花牛奶青团的售价为x元，根据销售额以及4月份鲜花牛奶青团和芒果青团总计销售个列出分式方程即可解答；

（2）设鲜花牛奶青团生产m个，芒果青团生产（12000-m）个，根据题意列出不等式，求出，设销售额为W元，表达出函数关系式，根据题意计算出a的取值范围，对a的值进行分类讨论，利用一次函数的增减性，确定方案即可．

解：（1）设芒果青团的售价为x元，则鲜花牛奶青团的售价为x元，则：

，

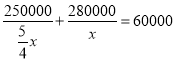解得：x=0.8，

经检验：x=0.8是原方程的解，

∴x=1，

∴芒果青团的售价为0.8元，则鲜花牛奶青团的售价为1元．

（2）设鲜花牛奶青团生产m个，芒果青团生产（12000-m）个，

由题意可得：，

解得：，

设销售额为W元，

则，

∵a＞0，且，则，

①当0＜a≤0.2时，0.2-a＞0，W随m的增大而增大，

∴当m=4800时，W最大，

②当a=0.2时，0.2-a=0，则无论如何设计，销售额不变；

③当0.2＜a≤0.4时，0.2-a＜0，W随m的增大而减小，

∴当m=4000时，W最大，

综上所述，当0＜a≤0.2时，鲜花牛奶青团生产4800个，芒果青团生产7200个，销售额最大；当a=0.2时，销售额不变；当0.2＜a≤0.4时，鲜花牛奶青团生产4000个，芒果青团生产8000个，销售额最大．

关闭