
【题目】如图,直线y=x+1与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=![]() .
.
(1)求k的值;
(2)设点N(1,a)是反比例函数y=![]() (x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】解:(1)由y=x+1可得A(0,1),即OA=1,
∵tan∠AHO=![]() =
=![]() ,
,
∴OH=2,
∵MH⊥x轴,
∴点M的横坐标为2,
∵点M在直线y=x+1上,
∴点M的纵坐标为3,即M(2,3),
∵点M在y=![]() 上,
上,
∴k=2×3=6;
(2)∵点N(1,a)在反比例函数y=![]() 的图象上,
的图象上,
∴a=6,即点N的坐标为(1,6),
过N作N关于y轴的对称点N1 , 连接MN1 , 交y轴于P(如图),
此时PM+PN最小,
∵N与N1关于y轴的对称,N点坐标为(1,6),
∴N1的坐标为(﹣1,6),
设直线MN1的解析式为y=kx+b,
把M,N1的坐标得![]() ,
,
解得:![]() ,
,
∴直线MN1的解析式为y=﹣x+5,
令x=0,得y=5,
∴P点坐标为(0,5).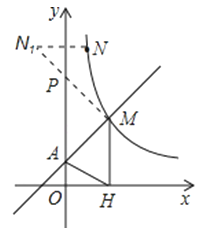
【解析】(1)对于直线y=x+1,令x=0求出y的值,确定出A坐标,得到OA的长,根据tan∠AHO的值,利用锐角三角函数定义求出OH的长,根据MH垂直于x轴,得到M横坐标与A横坐标相同,再由M在直线y=x+1上,确定出M坐标,代入反比例解析式求出k的值即可;
(2)将N坐标代入反比例解析式求出a的值,确定出N坐标,过N作N关于y轴的对称点N1 , 连接MN1 , 交y轴于P(如图),此时PM+PN最小,由N与N1关于y轴的对称,根据N坐标求出N1坐标,设直线MN1的解析式为y=kx+b,把M,N1的坐标代入求出k与b的值,确定出直线MN1的解析式,令x=0求出y的值,即可确定出P坐标.


科目:初中数学 来源: 题型:
【题目】清明节,除了扫墓踏青之外,传统时令小吃----青团也深受大家欢迎,知味观推出一款鲜花牛奶青团和一款芒果青团,鲜花牛奶青团每个售价是芒果青团的![]() 倍,4月份鲜花牛奶青团和芒果青团总计销售
倍,4月份鲜花牛奶青团和芒果青团总计销售![]() 个,鲜花牛奶青团销售额为
个,鲜花牛奶青团销售额为![]() 元,芒果青团销售额为
元,芒果青团销售额为![]() 元.
元.
(1)求鲜花牛奶青团和芒果青团的售价?
(2)5月份正值知味观店庆,决定再生产![]() 个青团回馈新老顾客,但考虑到芒果青团较受欢迎,同时也考虑受机器设备限制,因此芒果青团的个数不少于鲜花牛奶青团个数的
个青团回馈新老顾客,但考虑到芒果青团较受欢迎,同时也考虑受机器设备限制,因此芒果青团的个数不少于鲜花牛奶青团个数的![]() ,不多于鲜花牛奶青团的
,不多于鲜花牛奶青团的![]() 倍,其中,鲜花牛奶青团每个让利
倍,其中,鲜花牛奶青团每个让利![]() 元销售,芒果青团售价不变,并且让利后的鲜花牛奶青团售价不得低于芒果青团售价的
元销售,芒果青团售价不变,并且让利后的鲜花牛奶青团售价不得低于芒果青团售价的![]() ,问:知味观如何设计生产方案?使总销售额最大.
,问:知味观如何设计生产方案?使总销售额最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0, ![]() ).
).
(1)求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1 , △BA′O的面积为S2 , S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,
, ![]() 与
与![]() 互余,
互余, ![]() 平分
平分![]() .
.
(1)在图1中,若![]() ,则
,则![]() ______
______![]() ,
, ![]() ______
______![]() .
.
(2)在图1中,设![]() ,
, ![]() ,请探究
,请探究![]() 与
与![]() 之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);
之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);
(3)在已知条件不变的前提下,当![]() 绕着点O顺时针转动到如图2的位置,此时
绕着点O顺时针转动到如图2的位置,此时![]() 与
与![]() 之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时
之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时![]() 与
与![]() 之间的数量关系.
之间的数量关系.
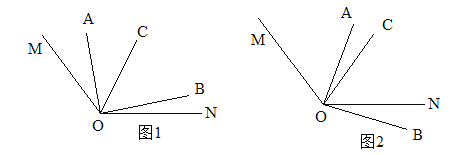
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y= ![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3, 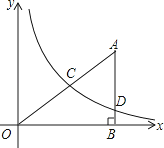
(1)求反比例函数y= ![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,双曲线y= ![]() 与直线y=﹣2x+2交于点A(﹣1,a).
与直线y=﹣2x+2交于点A(﹣1,a).
(1)求a,m的值;
(2)求该双曲线与直线y=﹣2x+2另一个交点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下面图象表示小红从家里出发去散步过程中离家的距离s(米)与散步所用的时间t(分)之间的关系,请根据图象,确定下面描述符合小红散步情景的是( )
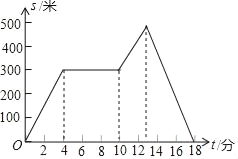
A. 从家出发,到了一个公共阅报栏,看了一会儿报,就回家了
B. 从家里出发,散了一会儿步,就找同学去了,18分钟后才开始返回
C. 从家里出发,一直散步(没有停留),然后回家了
D. 从家出发,到了一个公共阅报栏,看了一会儿报,继续向前走了一段后,然后回家了
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是圆0直径BD延长线上的一点,点C在圆0上,AC=BC,AD=CD.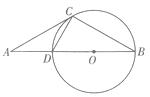
(1)求证:AC是圆0的切线;
(2)若⊙0的半径为2,求 ![]() ABC的面积.
ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com