
【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0, ![]() ).
).
(1)求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1 , △BA′O的面积为S2 , S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
【答案】
(1)
解:∵A(﹣1,0),B(0, ![]() ),
),
∴OA=1,OB= ![]() ,
,
在Rt△AOB中,tan∠BAO= ![]() =
= ![]() ,
,
∴∠BAO=60°
(2)
解:∵∠BAO=60°,∠AOB=90°,
∴∠ABO=30°,
∴CA'=AC= ![]() AB,
AB,
∴OA'=AA'=AO,
根据等边三角形的性质可得,△AOA'的边AO、AA'上的高相等,
∴△BA'O的面积和△AB'O的面积相等(等底等高的三角形的面积相等),
即S1=S2
(3)
解:S1=S2不发生变化;
理由:如图,过点'作A'M⊥OB.过点A作AN⊥OB'交B'O的延长线于N,
∵△A'B'O是由△ABO绕点O旋转得到,
∴BO=OB',AO=OA',
∵∠AON+∠BON=90°,∠A'OM+∠BON=180°﹣90°=90°,
∴∠AON=∠A'OM,
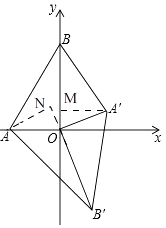
在△AON和△A'OM中, 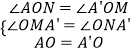 ,
,
∴△AON≌△A'OM(AAS),
∴AN=A'M,
∴△BOA'的面积和△AB'O的面积相等(等底等高的三角形的面积相等),
即S1=S2.
【解析】(1)先求出OA,OB,再用锐角三角函数即可得出结论;(2)根据等边三角形的性质可得AO=AA',再根据直角三角形30°角所对的直角边等于斜边的一半求出AO= ![]() AB,然后求出AO=OA',再根据等边三角形的性质求出点O到AB的距离等于点A'到AO的距离,然后根据等底等高的三角形的面积相等解答;(3)根据旋转的性质可得BO=OB',AA'=OA',再求出∠AON=∠A'OM,然后利用“角角边”证明△AON和△A'OM全等,根据全等三角形对应边相等可得AN=A'M,然后利用等底等高的三角形的面积相等证明.
AB,然后求出AO=OA',再根据等边三角形的性质求出点O到AB的距离等于点A'到AO的距离,然后根据等底等高的三角形的面积相等解答;(3)根据旋转的性质可得BO=OB',AA'=OA',再求出∠AON=∠A'OM,然后利用“角角边”证明△AON和△A'OM全等,根据全等三角形对应边相等可得AN=A'M,然后利用等底等高的三角形的面积相等证明.
【考点精析】认真审题,首先需要了解等边三角形的判定(三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形),还要掌握旋转的性质(①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°。将求∠AGD的过程填写完整,并将依据填到相应的括号内.

解:∵EF∥AD( )
∴∠2= 。( )
又∵∠1=∠2,( )
∴∠1=∠3。( )
∴AB∥ 。( )
∴∠BAC+ =180。( )
又∵∠BAC=70°,
∴∠AGD= 。
查看答案和解析>>
科目:初中数学 来源: 题型:
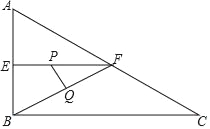
【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2cm,E、F分别是AB、AC的中点,动点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时动点Q从点B出发,沿BF方向匀速运动,速度为2cm/s,连接PQ,设运动时间为ts(0<t<1),则当t=___时,△PQF为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是 . 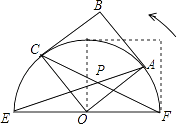
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
, ![]() ,
,![]() ,
,![]() , 垂足为
, 垂足为![]() ,在平行四边形的边上有一点
,在平行四边形的边上有一点![]() ,且
,且![]() .将平行四边形折叠,使点
.将平行四边形折叠,使点![]() 与点
与点![]() 合,折痕所在直线与平行四边形交于点
合,折痕所在直线与平行四边形交于点![]() 、
、![]() .
.

(1)求![]() 的长;
的长;
(2)请补全图形并求折痕![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
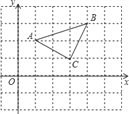
【题目】如图所示,三角形ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).
(1)三角形A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太仓港区道路绿化工程工地有大量货物需要运输,某车队有载重量为8吨和10吨的卡车共15辆,所有车辆运输一次能运输128吨货物.
(1)求该车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的扩大,车队需要一次运输货物170吨以上,为了完成任务,车队准备增购这两种卡车共5辆(两种车都购买),请写出所有可能的购车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人再次选择自行车作为出行工具,小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题: 
(1)a= , b= , m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是v米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出v的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com