
【题目】如图,点A是圆0直径BD延长线上的一点,点C在圆0上,AC=BC,AD=CD.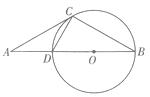
(1)求证:AC是圆0的切线;
(2)若⊙0的半径为2,求 ![]() ABC的面积.
ABC的面积.
【答案】
(1)证明:如图,连接OC . 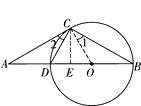
∵AC=BC , AD=CD , OB=OC ,
∴∠A=∠B=∠1=∠2.
∵∠ACO=∠DCO+∠2,
∴∠ACO=∠DCO+∠1=∠BCD .
又∵BD是直径,
∴∠BCD=90°,
∴∠ACO=90°,
又点C在⊙O上,
∴AC是⊙O的切线 。
(2)解:由题意可得△DCO是等腰三角形.
∵∠CDO=∠A+∠2,∠DOC=∠B+∠1,
∴∠CDO=∠DOC , 即△DCO是等边三角形,
∴∠A=∠B=∠1=∠2=30°,CD=AD=2.
在Rt△BCD中,BC= ![]() .
.
又AC=BC , ∴AC= ![]() .
.
如图,作CE⊥AB于点E .
在Rt△BEC中,∠B=30°,
∴CE= ![]() BC=
BC= ![]() ,
,
∴S△ABC= ![]() ABCE=
ABCE= ![]() ×6×
×6× ![]() =
= ![]() 。
。
【解析】(1)连接OC . 根据等边对等角得出∠A=∠B=∠1=∠2.根据角的和差及等量代换得出∠ACO=∠DCO+∠1=∠BCD .根据圆周角定理,直径所对的圆周角是直角得出∠BCD=90°,从而得出∠ACO=90°,又点C在⊙O上,根据切线的判定定理得出AC是⊙O的切线;
(2)根据三角形的外角定理得出∠CDO=∠A+∠2,∠DOC=∠B+∠1,又∠A=∠B=∠1=∠2.从而得出∠CDO=∠DOC,又△DCO是等腰三角形,从而得出△DCO是等边三角形,根据等边三角形的性质得出∠A=∠B=∠1=∠2=30°,CD=AD=2,然后由勾股定理得出BC的长度,又AC=BC,从而得出AC的长度,作CE⊥AB于点E . 根据含30°的直角三角形的边之间的关系得出CE的长,进而根据三角形的面积公式计算出结果。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=x+1与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=![]() .
.
(1)求k的值;
(2)设点N(1,a)是反比例函数y=![]() (x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠A=52°,若∠ABC与∠ACB的角平分线交于点D1,得到∠D1,∠ABD1与∠ACD1的角平分线交于点D2,得到∠D2;依此类推,∠ABD4与∠ACD4的角平分线交于点D5,得到∠D5,则∠D5的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只利用一把有刻度的直尺,用度量的方法按下列要求画图:
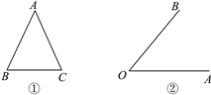
(1)在图①中用下面的方法画等腰三角形ABC的对称轴.
①量出底边BC的长度,将线段BC二等分,即画出BC的中点D;
②画直线AD,即画出等腰三角形ABC的对称轴.
(2)在图②中画∠AOB的对称轴,并写出画图的方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨l元,则每个月少卖l0件(每件售价不能高于65元).设每件商品的售价上x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量戈的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C按顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为( )
A.![]() π
π
B.![]() π
π
C.6π
D.![]() π
π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com