
【题目】如图,已知△ABC的三个顶点坐标分别为A(﹣1,﹣2),B(﹣1,﹣4),C(2,﹣3).
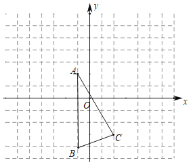
(1)将△ABC先向右平移4个单位,再向上平移6个单位,得到△A1B1C1,作出△A1B1C1,线段AC在平移过程中扫的面积为 ;
(2)作出△A1B1C1关于y轴对称的图形△A2B2C2,则坐标C2为 ;
(3)若△ABD与△ABC全等,则点D的坐标为 (点C与点D不重合)
【答案】(1)38;(2)(﹣6,3);(3)(2,1),(﹣4,1),(﹣4,﹣3).
【解析】
(1)利用点平移的坐标规律写出A1、B1、C1的坐标,然后连接即可,然后用一个矩形的面积分别减去四个直角三角形的面积去计算线段AC在平移过程中扫的面积;
(2)利用关于y轴对称的点的坐标特征写出A2、B2、C2的坐标,然后连接即可;
(3)根据全等三角形的性质确定D点坐标.
解:(1)如图,△A1B1C1为所作;线段AC在平移过程中扫的面积=11×7﹣2×![]() ×4×6﹣2×
×4×6﹣2×![]() ×5×3=38;
×5×3=38;
(2)如图,△A2B2C2为所作,点C2为的坐标为(﹣6,3);
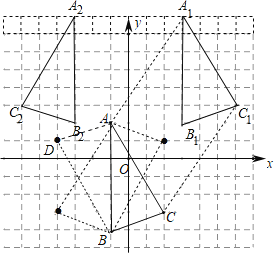
故答案为38;(﹣6,3);(2,1),(﹣4,1),(﹣4,﹣3).


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
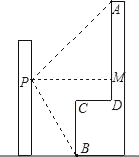
【题目】如图,李强在教学楼的点P处观察对面的办公大楼,为了求得对面办公大楼的高度,李强测得办公大楼顶部点A的仰角为30°,测得办公大楼底部点B的俯角为37°,已知测量点P到对面办公大楼上部AD的距离PM为30m,办公大楼平台CD=10m.求办公大楼的高度(结果保留整数).(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年2月14日,备受关注的《成都市中小学课后服务实施意见》正式出台.某区为了解“家长更希望如何安排孩子放学后的时间”,对该区七年级部分家长进行了一次问卷调查(每位同学只选择一位家长参与调查),将调查结果(![]() .回家,家人陪伴;
.回家,家人陪伴;![]() .学校课后延时服务;
.学校课后延时服务;![]() .校外培训机构;
.校外培训机构;![]() .社会托管班)绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
.社会托管班)绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
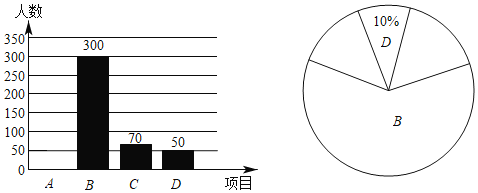
(1)本次调查的家长总人数为 ;
(2)补全条形统计图:扇形统计图中,![]() 类所对应的圆心角为 度;
类所对应的圆心角为 度;
(3)若该区共有七年级学生![]() 人,则愿意参加“学生课后延时服务”的人数大概是多少?
人,则愿意参加“学生课后延时服务”的人数大概是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,请你判断∠1+∠2与∠A有何数量关系,直接写出你的结论,不必说明理由
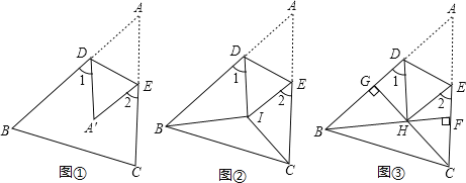
思考(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=100°,求∠BIC的度数;
拓展(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC=BC,∠ACB=90°,AE平分∠BAC交BC于点D,BF⊥AE,交AC的延长线于点F,且垂足为E,则下列结论①AD=BF;②BF=AF;③AC+CD=AB;④AB=BF:⑤AD=2BE.其中正确的结论有( )个
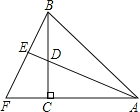
A. 5B. 4C. 3D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
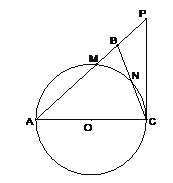
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
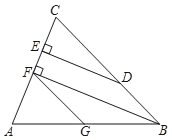
【题目】已知:如图,DE⊥AC,垂足为点E,∠AGF=∠ABC,∠BFG+∠BDE=180°,
求证:BF⊥AC.
请完成下面的证明的过程,并在括号内注明理由.
证明:∵∠AGF=∠ABC(已知)
∴FG∥ ( )
∴∠BFG=∠FBC( )
∵∠BFG+∠BDE=180°(已知)
∴∠FBC+∠BDE=180°( )
∴BF∥DE( )
∴∠BFA= (两直线平行,同位角相等)
∵DE⊥AC(已知)
∴∠DEA=90°( )
∴∠BFA=90°(等量代换)
∴BF⊥AC(垂直的定义)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com