
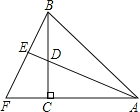
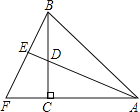
【题目】如图,AC=BC,∠ACB=90°,AE平分∠BAC交BC于点D,BF⊥AE,交AC的延长线于点F,且垂足为E,则下列结论①AD=BF;②BF=AF;③AC+CD=AB;④AB=BF:⑤AD=2BE.其中正确的结论有( )个
A. 5B. 4C. 3D. 2
【答案】C
【解析】
根据∠ACB=90°,BF⊥AE,得出∠ACB=∠BED=∠BCF=90°,推出∠F=∠ADC,证△BCF≌△ACD,根据全等三角形的性质即可判断①②;假如AC+CD=AB,求出∠F+∠FBC=90°,即可判断③④,证根据全等三角形的判定ASA得出△BEA≌△FEA,推出BE=EF,即可判断⑤.
解:∵∠ACB=90°,BF⊥AE,
∴∠ACB=∠BED=∠BCF=90°,
∴∠F+∠FBC=90°,∠BDE+∠FBC=90°,
∴∠F=∠BDE,
∵∠BDE=∠ADC,
∴∠F=∠ADC,
∵AC=BC,
∴△BCF≌△ACD,
∴AD=BF,∴①正确;
∵AF>AD,
∴BF≠AF②错误;
∵△BCF≌△ACD,
∴CD=CF,
∴AC+CD=AF,
∵△BCF≌△ACD,
∴CD=CF,
∴AC+CD=AF,
又∵AB=AF,
∴AC+CD=AB.
∴③正确;
∵BF=AC,AC<AF=AB,
∴AB>BF,
∴④错误;
由△BCF≌△ACD,
∴AD=BF,
∵AE平分∠BAF,AE⊥BF,
∴∠BEA=∠FEA=90°,∠BAE=∠FAE,
∵AE=AE,∴△BEA≌△FEA,
∴BE=EF,
∴⑤正确;
综上所述,正确的结论是:①③⑤,共有3个.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )

A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,AC分别是半⊙O的直径和弦,OD⊥AC于点D,过点A作半⊙O的切线AP,AP与OD的延长线交于点P.连接PC并延长与AB的延长线交于点F.
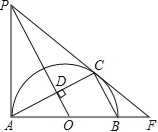
(1)求证:PC是半⊙O的切线;
(2)若∠CAB=30°,AB=10,求线段BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(m-1)x2-x-2=0.
(1)若x=-1是方程的一个根,求m的值和方程的另一根;
(2)当m为何实数时,方程有两个不相等的实数根?
(3)若x1,x2是方程的两个实数根,且xx2+x1x=-![]() ,试求实数m的值.
,试求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将挂好彩旗的旗杆垂直插在操场上,旗杆从旗顶到地面的高度为320cm,在无风的天气里,彩旗自然下垂,如图所示,
(1)求彩旗下垂时最低处离地面的最小高度h.彩旗完全展平时的尺寸如图的长方形(单位:cm)
(2)商店彩旗的标价为每面40元,旗杆的标价为每根20元,学校计划购买彩旗60面,旗杆50根,由于数量较多商店决定给予学校优惠,其中彩旗每面优惠10%,旗杆每根优惠![]() a%,这样,学校彩旗又多购买了2a%,旗杆的数量不变,这样总共花费3542元,求a的值.
a%,这样,学校彩旗又多购买了2a%,旗杆的数量不变,这样总共花费3542元,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点坐标分别为A(﹣1,﹣2),B(﹣1,﹣4),C(2,﹣3).
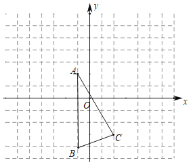
(1)将△ABC先向右平移4个单位,再向上平移6个单位,得到△A1B1C1,作出△A1B1C1,线段AC在平移过程中扫的面积为 ;
(2)作出△A1B1C1关于y轴对称的图形△A2B2C2,则坐标C2为 ;
(3)若△ABD与△ABC全等,则点D的坐标为 (点C与点D不重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=![]() 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=![]() 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点P.
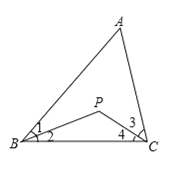
(1)当∠A=40°,∠ABC=60°时,求∠BPC的度数;
(2)当∠A=α°时,求∠BPC的度数.(用α的代数式表示)
(3)小明研究时发现:如果延长AB至D,再过点B作BQ⊥BP,那么BQ就是∠CBD的平分线。请你证明小明的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.

(1)求BD·cos∠HBD的值;
(2)若∠CBD=∠A,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com