
【题目】课上老师提出一个问题:“如图,已知![]() ,
,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 的度数.”
的度数.”
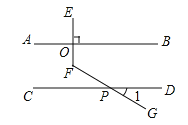
甲、乙、丙三位同学用不同的方法添加辅助线解决问题如图1,图2,图3所示.
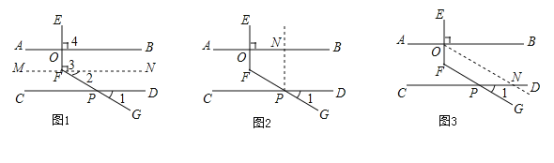
(1)补全甲同学的分析思路.
辅助线:过点![]() 作
作![]() .
.
分析思路:
①欲求∠EFG的度数,由图可知只需转化为求________和___________的度数之和;
②由辅助线作图可知![]() ;
;
③由![]() ,
,![]() 推出_________________,由此可推出
推出_________________,由此可推出![]() ;
;
④由已知![]() ,可得
,可得![]() ,所以可得
,所以可得![]() 的度数,从而可求
的度数,从而可求![]() 的度数.
的度数.
(2)请你根据乙同学所画的辅助线,补全求解过程.
解:过![]() 作___________________,交
作___________________,交![]() 于点
于点![]() .
.
![]() ___________________________
___________________________![]() (两直线平行,同位角相等).
(两直线平行,同位角相等).
![]() ,
,
![]() ,
,
![]() (_______________________).
(_______________________).
![]() .
.
![]() (____________________________),
(____________________________),
![]() ,
,
![]() _______________________.
_______________________.
(3)请你根据丙同学所画的辅助线,求![]() 的度数.
的度数.
【答案】(1)∠2;∠3;AB∥MN;(2)NP∥EF;∠NPG;两直线平行,同位角相等;两直线平行,同旁内角互补;120°;(3)∠EFG=120°
【解析】
(1)根据已作辅助线及平行于同一条直线的两条直线平行即可解答;
(2)根据垂线的定义以及平行线的性质即可解答;
(3)根据平行线的性质即可解答.
解:(1)∵∠EFG=∠2+∠3,
∴欲求∠EFG的度数,由图可知只需转化为求∠2和∠3的度数之和;
由![]() ,
,![]() 推出AB∥MN,
推出AB∥MN,
故答案为:∠2;∠3;AB∥MN.
(2)过![]() 作NP∥EF,交
作NP∥EF,交![]() 于点
于点![]() .
.
∴∠NPG![]() (两直线平行,同位角相等).
(两直线平行,同位角相等).
![]() ,
,
![]() ,
,
![]() (两直线平行,同位角相等).
(两直线平行,同位角相等).
![]() .
.
∴![]() (两直线平行,同旁内角互补),
(两直线平行,同旁内角互补),
![]() ,
,
![]() 120°.
120°.
故答案为:NP∥EF;∠NPG;两直线平行,同位角相等;两直线平行,同旁内角互补;120°
(3)如图,过点O作ON∥FG,
∵ON∥FG,
∴∠EFG=∠EON,∠1=∠ONC=30°,
∵AB∥CD,
∴∠ONC=∠BON=30°,
∵EF⊥AB
∴∠EOB=90°,
∴∠EFG=∠EON=∠EOB+∠BON=90°+30°=120°.


科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )

A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)平面上有四个点A,B,C,D,按照以下要求作图:
①作直线AD;
②作射线CB交直线AD于点E;
③连接AC,BD交于点F;
(2)图中共有 条线段;
(3)若图中F是AC的一个三等分点,AF<FC,已知线段AC上所有线段之和为18,求AF长.
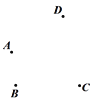
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() .
.
(1)若![]() ,
,![]() 平分
平分![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
①求证![]() ;
;
②将结论![]() 与条件
与条件![]() 互换位置,其他条件不变,组成一个新的命题,判断该命题的真假,并写出证明过程.
互换位置,其他条件不变,组成一个新的命题,判断该命题的真假,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理探索:(1)数轴上点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分别表示数0、 2 、3、5、 4 ,解答下列问题.
分别表示数0、 2 、3、5、 4 ,解答下列问题.
①画出数轴表示出点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ;
;
![]()
②![]() 、
、![]() 两点之间的距离是 ;
两点之间的距离是 ;
③![]() 、
、![]() 两点之间的距离是 ;
两点之间的距离是 ;
④![]() 、
、 ![]() 两点之间的距离是 ;
两点之间的距离是 ;
(2)请思考,若点![]() 表示数
表示数![]() 且
且![]() ,点
,点 ![]() 表示数
表示数![]() ,且
,且 ![]() ,则用含
,则用含 ![]() ,
,![]() 的代数式表示
的代数式表示 ![]() 、
、![]() 两点 间的距离是 ;
两点 间的距离是 ;
(3)请归纳,若点![]() 表示数
表示数![]() ,点
,点 ![]() 表示数
表示数![]() ,则
,则 ![]() 、
、![]() 两点间的距离用含
两点间的距离用含![]() 、
、![]() 的代数式表示是 .
的代数式表示是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,AC分别是半⊙O的直径和弦,OD⊥AC于点D,过点A作半⊙O的切线AP,AP与OD的延长线交于点P.连接PC并延长与AB的延长线交于点F.
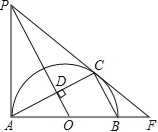
(1)求证:PC是半⊙O的切线;
(2)若∠CAB=30°,AB=10,求线段BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(m-1)x2-x-2=0.
(1)若x=-1是方程的一个根,求m的值和方程的另一根;
(2)当m为何实数时,方程有两个不相等的实数根?
(3)若x1,x2是方程的两个实数根,且xx2+x1x=-![]() ,试求实数m的值.
,试求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
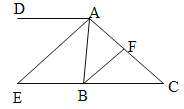
【题目】如图,已知在△ABC中,∠ABC与∠ACB的平分线交于点P.
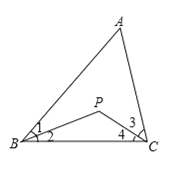
(1)当∠A=40°,∠ABC=60°时,求∠BPC的度数;
(2)当∠A=α°时,求∠BPC的度数.(用α的代数式表示)
(3)小明研究时发现:如果延长AB至D,再过点B作BQ⊥BP,那么BQ就是∠CBD的平分线。请你证明小明的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com