
【题目】在平面直角坐标系中,已知点A![]() ,点B
,点B![]() ,点C是y轴上的一个动点,当∠BCA=30°时,点C的坐标为______.
,点C是y轴上的一个动点,当∠BCA=30°时,点C的坐标为______.
【答案】(0,![]() ),(0,
),(0,![]() )
)
【解析】
(1)如图1,以AB为边在x轴的上方作等边△PAB,再以点P为圆心,PA为半径作圆P,交y轴的正半轴于点C,连接BC、AC,则此时∠BCA=30°,再根据题中的已知条件求得线段OC的长,即可得到此时点C的坐标;
(2)如图2,和(1)同理在y轴的负半轴可求得另一个符合要求的点C的坐标.
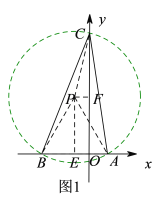
(1)如图1,以AB为边在x轴的上方作等边△PAB,则∠APB=60°,再以点P为圆心,PA为半径作圆P,交y轴的正半轴于点C,连接BC、AC,则此时由∠APB=60°可得∠BCA=30°,
∵点A、B的坐标分别为:![]() ,
,![]() ,
,
∴AB=![]() ,OB=
,OB=![]()
∴PA=PC=AB=![]() ,
,
过点P作PF⊥y轴于点F,PE⊥x轴于点E,则四边形PEOF是矩形,
∴OF=PE,PF=OE,
∵在等边△PAB中,PE=PA·sin60°=![]() ,BE=
,BE=![]() AB=
AB=![]() ,
,
∴OF=12,OE=OB-BE=![]() ,
,
∴PF=![]() ,
,
又∵在Rt△PFC中,PC=![]() ,∠PFC=90°,
,∠PFC=90°,
∴CF=![]() ,
,
∴OC=OF+CF=![]() ,
,
∴此时点C的坐标为![]() ;
;
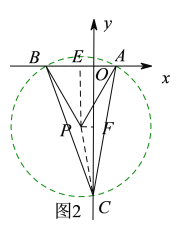
(2)如图2,以AB为边在x轴的下方作等边△PAB,则∠APB=60°,再以点P为圆心,PA为半径作圆P,交y轴的负半轴于点C,连接BC、AC,则此时由∠APB=60°可得∠BCA=30°,和(1)同理可得此时点C的坐标为:![]() ;
;
综上所述,符合条件的点![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】快、慢两车分别从相距480km路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1h,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车调头的时间忽略不计),快、慢两车距乙地的路程ykm与所用时间xh之间的函数图像如图所示,请结合图像信息解答下列问题:
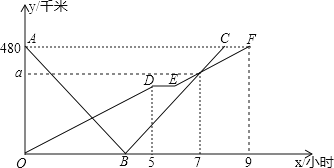
(1)直接写出慢车的行驶速度和a的值;
(2)求快车的速度和B点坐标;
(3)快车和慢车第一次相遇时,距离甲地的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;
(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
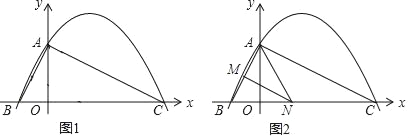
查看答案和解析>>
科目:初中数学 来源: 题型:
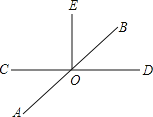
【题目】已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90,AB=6,BC=8.以AB, BC,AC的中点A1,B1,C1构成△A1B1C1,以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2,……依次操作,阴影部分面积之和将接近 ( )

A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线L1:y1=x2+6x+5k和抛物线L2:y2=kx2+6kx+5k,其中k≠0.
(1)下列说法你认为正确的是(填写序号) ;
①抛物线L1和L2与y轴交于同一点(0,5k);
②抛物线L1和L2开口都向上;
③抛物线L1和L2的对称轴是同一条直线;
④当k<-1时,抛物线L1和L2都与x轴有两个交点.
(2)抛物线L1和L2相交于点E、F,当k的值发生变化时,请判断线段EF的长度是否发生变化,并说明理由;
(3)在(2)中,若抛物线L1的顶点为M,抛物线L2的顶点为N,问是否存在实数k,使MN=2EF?如存在,求出实数k;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读下面材料:如果![]() (
(![]() )的b次幂等于N,即有指数式
)的b次幂等于N,即有指数式![]() ,那么数b叫做以
,那么数b叫做以![]() 为底N的对数,
为底N的对数,
记作:对数式: ![]()
例如:
(1)因为指数式![]() ,所以以2为底,4的对数是2,对数式记作:
,所以以2为底,4的对数是2,对数式记作:![]()
(2)因为指数式![]() ,所以以4为底,16的对数是2,对数式记作:
,所以以4为底,16的对数是2,对数式记作:![]()
1. 请根据上面阅读材料将下列指数式改为对数试:(1)![]() ;(2)
;(2)![]()
2. 将下列对数式改为指数式:(1)![]() ;(2)
;(2)![]()
3.计算 :![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课上老师提出一个问题:“如图,已知![]() ,
,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 的度数.”
的度数.”
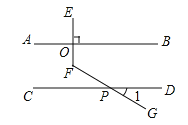
甲、乙、丙三位同学用不同的方法添加辅助线解决问题如图1,图2,图3所示.
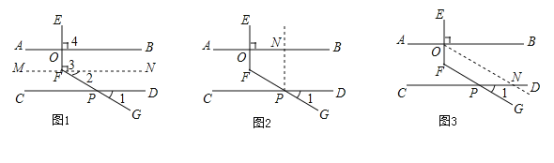
(1)补全甲同学的分析思路.
辅助线:过点![]() 作
作![]() .
.
分析思路:
①欲求∠EFG的度数,由图可知只需转化为求________和___________的度数之和;
②由辅助线作图可知![]() ;
;
③由![]() ,
,![]() 推出_________________,由此可推出
推出_________________,由此可推出![]() ;
;
④由已知![]() ,可得
,可得![]() ,所以可得
,所以可得![]() 的度数,从而可求
的度数,从而可求![]() 的度数.
的度数.
(2)请你根据乙同学所画的辅助线,补全求解过程.
解:过![]() 作___________________,交
作___________________,交![]() 于点
于点![]() .
.
![]() ___________________________
___________________________![]() (两直线平行,同位角相等).
(两直线平行,同位角相等).
![]() ,
,
![]() ,
,
![]() (_______________________).
(_______________________).
![]() .
.
![]() (____________________________),
(____________________________),
![]() ,
,
![]() _______________________.
_______________________.
(3)请你根据丙同学所画的辅助线,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com