
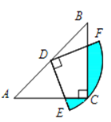
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=![]() ,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为_______.
,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为_______.
【答案】![]()
【解析】
根据题意作出合适的辅助线,可知阴影部分的面积等于扇形DEF的面积与四边形DNCM的面积之差,而四边形DNCM的面积等于三角形CDB的面积,再根据题目中的数据即可解答本题.
连接CD,设DF交BC于M,DE交AC于N,如图所示,
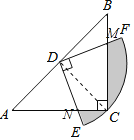
∵以AB中点D为圆心,作圆心角为90°的扇形DEF,点C恰好在弧EF上,
∴CD=![]() AB=2
AB=2![]() ,∠B=∠DCN=45°,CD=BD,
,∠B=∠DCN=45°,CD=BD,
∵∠ADC=∠BDC=∠EDF=90°,
∴∠EDC+∠CDF=90°,∠CDF+∠BDF=90°,
∴∠BDM=∠CDN,
在△BDM和△CDN中,
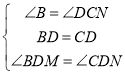 ,
,
∴△BDM≌△CDN(ASA),
∴△CDN与△CDM的面积之和等于△CDM与△BDM的面积之和,
即四边形DNCM的面积等于△CDB的面积,
∴阴影部分的面积是: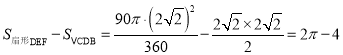 ,
,
故答案为:![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】如图1所示在矩形ABCD中,AB=6,AD=3,点E、F分别是边DC、DA的三等分点(DE![]() EC,DF
EC,DF![]() AF),四边形DFGE为矩形,连接BG.
AF),四边形DFGE为矩形,连接BG.
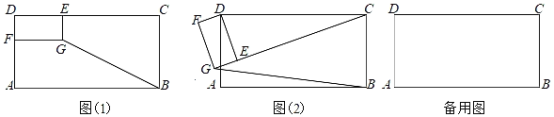
(1)问题发现:在图(1)中,![]() = ;
= ;
(2)拓展探究:将图(1)中的矩形DFGE绕点D旋转一周,在旋转过程中![]() 的大小有无变化?请仅就图(2)的情形给出证明;
的大小有无变化?请仅就图(2)的情形给出证明;
(3)问题解决:当矩形DFGE旋转至B、G、E三点共线时,请直接写出线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:①AC垂直平分DE;②△CDE为等边三角形;③tan∠BCD=![]() ;④
;④![]() ,其中正确的结论是____________ (填写所有正确结论的序号)
,其中正确的结论是____________ (填写所有正确结论的序号)
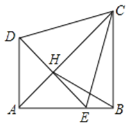
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部有一块广告牌![]() ,小背在山坡的坡脚
,小背在山坡的坡脚![]() 处测得广告牌底部的仰角为45°,沿坡面
处测得广告牌底部的仰角为45°,沿坡面![]() 向上走到
向上走到![]() 处测得广告牌顶部
处测得广告牌顶部![]() 的仰角为30°.已知山坡
的仰角为30°.已知山坡![]() 的坡度为
的坡度为![]() ,
,![]() 米,
米,![]() 米.
米.
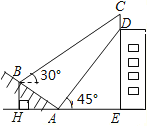
此题考查了折叠的性质、矩形的性质、全等三角形的判定与性质以及勾股定理的应用.熟练掌握折叠的性质是关键.
(1)求点![]() 距地面的高度
距地面的高度![]() ;
;
(2)求广告牌![]() 的高度.(结果保留根号)
的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
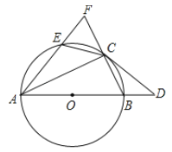
【题目】如图,E为圆O上的一点,C为劣弧EB的中点.CD切![]() 于点C,交
于点C,交![]() 的直径AB的延长线于点D.延长线段AE和线段BC,使之交于点F.
的直径AB的延长线于点D.延长线段AE和线段BC,使之交于点F.
(1)求证:![]() 和
和![]() 都是等腰三角形;
都是等腰三角形;
(3)若![]() ,
,![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,点E是射线AD上的一个动点(不与点A重合)将线段AE绕点A顺时针旋转90°得到线段AF,连接CF交线段AB于点G,交AD于点H、连接EG.
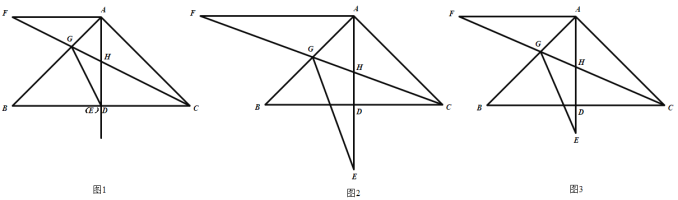
特例分析:
(1)如图1,当点E与点D重合时,“智敏”小组提出如下问题,请你解答:
①求证:AF=CD;
②用等式表示线段CG与EG之间的数量关系为:_______;
拓展探究:
(2)如图2,当点E在线段AD的延长线上,且DE=AD时,“博睿”小组发现CF=2EG.请你证明;
(3)如图3,当点E在线段AD的延长线上,且AE=AB时,![]() 的值为_______;
的值为_______;
推广应用:
(4)当点E在射线AD上运动时,![]() ,则
,则![]() 的值为______用含m.n的式子表示).
的值为______用含m.n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月,“亚洲文明对话大会”在北京成功举办,某研究机构为了了解10-60岁年年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将搜集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第一组 |
| 5 |
第二组 |
|
|
第三组 |
| 35 |
第四组 |
| 20 |
第五组 |
| 15 |
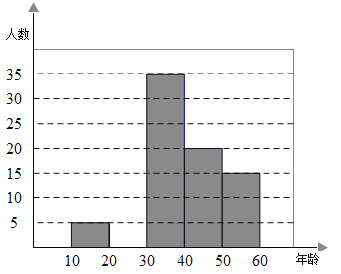

请直接写出第3组人数在扇形统计图中所对应的圆心角是_________度;假设该市现有10-60岁的市民300万人,则40-50岁年龄段的关注本次大会的人数约有___________万人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点P是平行四边形ABCD外一点,PE∥AB交BC于点E.PA、PD分别交BC于点M、N,点M是BE的中点.
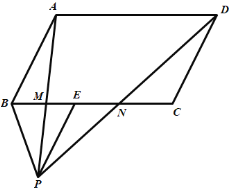
(1)求证:CN=EN;
(2)若平行四边形ABCD的面积为12,求△PMN的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com