
【题目】如图,抛物线![]() 经过点A(4,0)、B(1,0),交y轴于点C.
经过点A(4,0)、B(1,0),交y轴于点C.
(1)求抛物线的解析式.
(2)点P是直线AC上方的抛物线上一点,过点P作![]() 于点H,求线段PH长度的最大值.
于点H,求线段PH长度的最大值.
(3)Q为抛物线上的一个动点(不与点A、B、C重合),![]() 轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
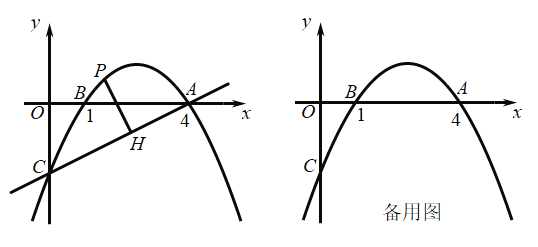
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)根据待定系数法解答即可;
(2)先利用待定系数法求出直线AC的解析式,过点 P 作 x 轴的垂线,交直线 AC 于点 E,如图1,设点P的横坐标为t,则PE可用含t的代数式表示,易证△PEH∽△ACO,可得![]() ,于是PH可用含t的代数式表示,然后根据二次函数的性质即可求出PH长度的最大值;
,于是PH可用含t的代数式表示,然后根据二次函数的性质即可求出PH长度的最大值;
(3)设Q点的横坐标为m,则Q点的纵坐标可用m的代数式表示,分三种情况:当1<m<4时,如图2;当m>4时,如图3;当m<1时,如图4,根据相似三角形的性质分![]() 与
与![]() 两种情况,建立关于m的方程求解即可.
两种情况,建立关于m的方程求解即可.
解:(1)将 A(4,0)、B(1,0)代入![]() ,
,
得:![]() ,解得
,解得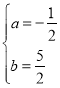 ,
,
∴抛物线的解析式为![]() ;
;
(2)将![]() 代入
代入![]() ,得
,得![]() ,∴
,∴![]() .
.
设直线 AC 的解析式为![]() ,
,
将 A(4,0)代入![]() ,解得:
,解得:![]() ,
,
∴直线 AC 的解析式为![]() .
.
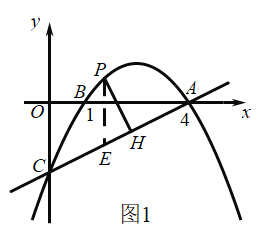
过点 P 作 x 轴的垂线,交直线 AC 于点 E,如图1,
设 ![]() ,则
,则![]() .
.
∴![]() .
.
∵∠PEH=∠ACO,∠PHE=∠AOC=90°,
∴△PEH∽△ACO,
∴![]() ,
,
∴![]() .
.
∴当![]() 时,PH 有最大值
时,PH 有最大值![]() ;
;
(3)存在,点![]() 或
或![]() 或
或![]() .
.
理由如下:
设Q点的横坐标为m,则Q点的纵坐标为﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
当1<m<4时,如图2,AM=4﹣m,QM=﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
又∵∠COA=∠QMA=90°,
∴①当![]() 时,△AQM∽△ACO,即4﹣m=2(﹣
时,△AQM∽△ACO,即4﹣m=2(﹣![]() m2+
m2+![]() m﹣2),
m﹣2),
解得:m=2或m=4(舍去),
此时Q(2,1);
②当![]() 时,△AQM∽△CAO,即2(4﹣m)=﹣
时,△AQM∽△CAO,即2(4﹣m)=﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
解得:m=4或m=5(均不合题意,舍去);
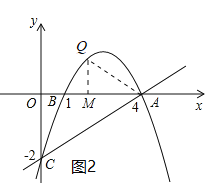
当m>4时,如图3,AM=m-4,QM=![]() m2-
m2-![]() m+2,
m+2,
又∵∠COA=∠QMA=90°,
∴①当![]() 时,△AQM∽△ACO,即m-4=2(
时,△AQM∽△ACO,即m-4=2(![]() m2-
m2-![]() m+2),
m+2),
解得:m=2或m=4(均不合题意,舍去);
②当![]() 时,△AQM∽△CAO,即2(m-4)=
时,△AQM∽△CAO,即2(m-4)=![]() m2-
m2-![]() m+2,
m+2,
解得:m=5或m=4(不合题意,舍去);
∴Q(5,﹣2);
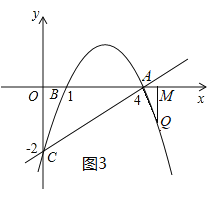
当m<1时,如图4,AM=4-m,QM=![]() m2-
m2-![]() m+2,
m+2,
又∵∠COA=∠QMA=90°,
①当![]() 时,△AQM∽△ACO,即4﹣m=2(
时,△AQM∽△ACO,即4﹣m=2(![]() m2-
m2-![]() m+2),
m+2),
解得:m=0或m=4(均不合题意,舍去);
②当![]() 时,△AQM∽△CAO,即2(4﹣m)=
时,△AQM∽△CAO,即2(4﹣m)=![]() m2-
m2-![]() m+2,
m+2,
解得:m=﹣3或m=4(不合题意,舍去);
∴Q(﹣3,﹣14);
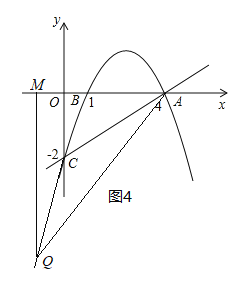
综上所述,符合条件的点Q为(2,1)或(5,﹣2)或(﹣3,﹣14).


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】2012年6月5日是“世界环境日”,南宁市某校举行了“绿色家园”演讲比赛,赛后整理参赛同学的成绩,制作成直方图(如图).
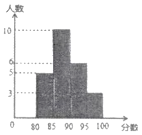
(1)分数段在______范围的人数最多;
(2)全校共有________人参加比赛;
(3)学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛,并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子.请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果,并求出上衣和能搭配成同一种颜色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
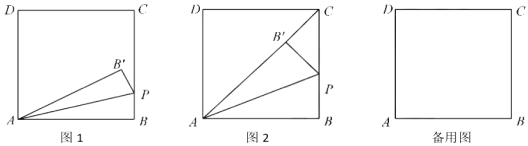
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
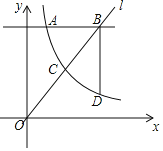
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(1)求反比例函数的解析式;
(2)当BD=2AB时,求点B的坐标;
(3)在(2)的条件下,直接写出不等式![]() >mx的解集.
>mx的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解九年级的600名学生每天的自主学习情况,随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两副不完整的统计图(图1图2),请根据统计图中的信息回答下列问题:
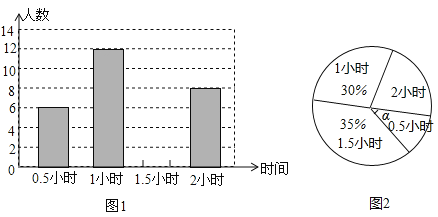
(1)本次调查的学生人数是 人;
(2)图2中角![]() 是 度;
是 度;
(3)将图1条形统计图补充完整;
(4)估算该校九年级学生自主学习不少于1.5小时有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
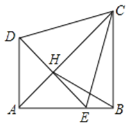
【题目】将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:①AC垂直平分DE;②△CDE为等边三角形;③tan∠BCD=![]() ;④
;④![]() ,其中正确的结论是____________ (填写所有正确结论的序号)
,其中正确的结论是____________ (填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差.根据表中数据,要从中选择一名成绩好且发挥稳定的同学参加数学竞赛,应该选择__________(填“甲”, “乙”, “丙”, “丁”).
甲 | 乙 | 丙 | 丁 | |
平均数(分) | 92 | 95 | 95 | 92 |
方差 | 3.6 | 3.6 | 7.4 | 8.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
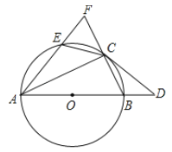
【题目】如图,E为圆O上的一点,C为劣弧EB的中点.CD切![]() 于点C,交
于点C,交![]() 的直径AB的延长线于点D.延长线段AE和线段BC,使之交于点F.
的直径AB的延长线于点D.延长线段AE和线段BC,使之交于点F.
(1)求证:![]() 和
和![]() 都是等腰三角形;
都是等腰三角形;
(3)若![]() ,
,![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,![]() ,
,![]() ,AB和CD之间的距离是8,动点P在线段AB上从点A出发沿AB方向以每秒2个单位的速度匀速运动;动点Q在线段BC上从点B出发沿BC的方向以每秒1个单位的速度匀速运动,过点P作
,AB和CD之间的距离是8,动点P在线段AB上从点A出发沿AB方向以每秒2个单位的速度匀速运动;动点Q在线段BC上从点B出发沿BC的方向以每秒1个单位的速度匀速运动,过点P作![]() ,交线段AD于点E,若
,交线段AD于点E,若![]() 两点同时出发,设运动时间为
两点同时出发,设运动时间为![]() 秒,
秒,![]() .
.
(1)当![]() 为何值时,BE平分
为何值时,BE平分![]() ?
?
(2)连接PQ,CE,设四边形PECQ的面积为S,求出S与![]() 的函数关系式;
的函数关系式;
(3)是否存在某一时刻![]() ,使得
,使得![]() ?若存在,请直接给出此时
?若存在,请直接给出此时![]() 的值(不必写说理过程);若不存在,请说明理由.
的值(不必写说理过程);若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com