
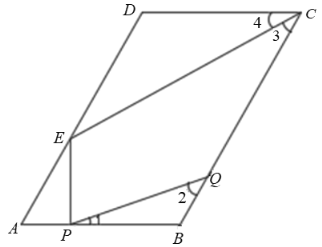
【题目】如图,在平行四边形ABCD中,![]() ,
,![]() ,AB和CD之间的距离是8,动点P在线段AB上从点A出发沿AB方向以每秒2个单位的速度匀速运动;动点Q在线段BC上从点B出发沿BC的方向以每秒1个单位的速度匀速运动,过点P作
,AB和CD之间的距离是8,动点P在线段AB上从点A出发沿AB方向以每秒2个单位的速度匀速运动;动点Q在线段BC上从点B出发沿BC的方向以每秒1个单位的速度匀速运动,过点P作![]() ,交线段AD于点E,若
,交线段AD于点E,若![]() 两点同时出发,设运动时间为
两点同时出发,设运动时间为![]() 秒,
秒,![]() .
.
(1)当![]() 为何值时,BE平分
为何值时,BE平分![]() ?
?
(2)连接PQ,CE,设四边形PECQ的面积为S,求出S与![]() 的函数关系式;
的函数关系式;
(3)是否存在某一时刻![]() ,使得
,使得![]() ?若存在,请直接给出此时
?若存在,请直接给出此时![]() 的值(不必写说理过程);若不存在,请说明理由.
的值(不必写说理过程);若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
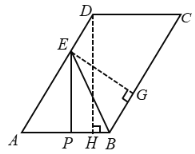
(1)过点D作DH⊥AB,过点E作![]() 于点G,证明
于点G,证明![]() 求得
求得![]() ,由角平分线的性质可得
,由角平分线的性质可得![]() ,再利用面积法求出
,再利用面积法求出![]() ,从而可得方程
,从而可得方程![]() ,求解即可;
,求解即可;
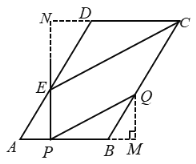
(2)过点Q作![]() 交AB的延长线于点M,延长PE,CD相交于点N,证明
交AB的延长线于点M,延长PE,CD相交于点N,证明![]() ,求得
,求得![]() ,求得
,求得![]()
![]() ,再求得
,再求得![]() ,
,![]() ,利用
,利用![]() 求解即可;
求解即可;
(3)由![]() 和四边形ABCD是平行四边形可证明
和四边形ABCD是平行四边形可证明![]() ,得
,得![]() ,得出
,得出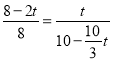 ,求解方程即可.
,求解方程即可.
(1)过点D作DH⊥AB,过点E作![]() 于点G,
于点G,
![]()
由题意得,![]() ,
,![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 平分
平分![]()
![]()
∵四边形ABCD是平行四边形
![]()
∵S四边形ABCD=![]()
![]()
![]()
![]()
即![]() 时,BE平分
时,BE平分![]()
(2)过点Q作![]() 交AB的延长线于点M,延长PE,CD相交于点N,
交AB的延长线于点M,延长PE,CD相交于点N,
由题意得,![]() ,
,![]()
由(1)知,![]()
在![]() 中,
中,![]()
![]()
∵四边形ABCD是平行四边形
![]()
![]()
![]()
![]()
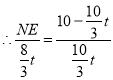
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
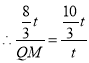
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3)假设存在t使得![]()
由(2)知,![]() ,
,![]() ,
,![]() ,
,
∵四边形ABCD是平行四边形,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
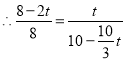
化简得,![]()
解得:![]()
![]()
![]()
经检验,![]() 是原方程的解,符合题意,
是原方程的解,符合题意,
即存在t使得CE//QP,此时![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点A(4,0)、B(1,0),交y轴于点C.
经过点A(4,0)、B(1,0),交y轴于点C.
(1)求抛物线的解析式.
(2)点P是直线AC上方的抛物线上一点,过点P作![]() 于点H,求线段PH长度的最大值.
于点H,求线段PH长度的最大值.
(3)Q为抛物线上的一个动点(不与点A、B、C重合),![]() 轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
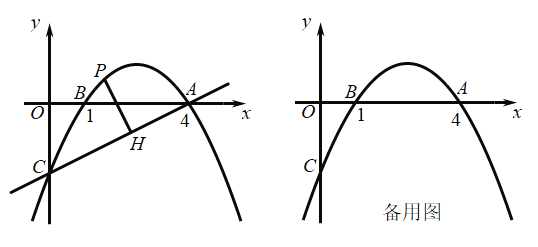
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳OB的长为3m,静止时,踏板到地面距离BD的长为0.6m(踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为hm,成人的“安全高度”为2m(计算结果精确到0.1m)
(1)当摆绳OA与OB成45°夹角时,恰为儿童的安全高度,则h= m
(2)某成人在玩秋千时,摆绳OC与OB的最大夹角为55°,问此人是否安全?(参考数据:![]() ≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
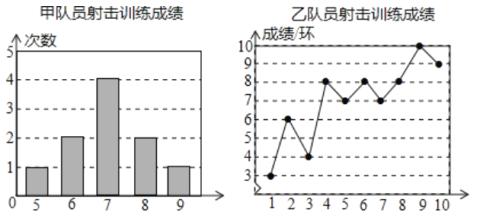
根据以上信息,整理分析数据如下:
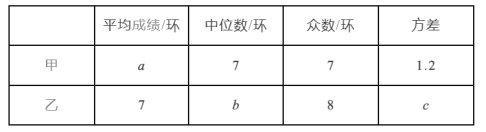
(1)写出表格中![]() 的值;
的值;
(2)综合运用上表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应该选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
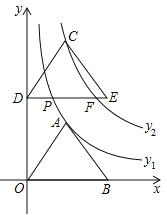
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在第一象限,点
在第一象限,点![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .把
.把![]() 向上平移
向上平移![]() 个单位长度得到
个单位长度得到![]() .反比例函数
.反比例函数![]() 的图象经过点
的图象经过点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设反比例函数![]() 的图象交线段
的图象交线段![]() 于点
于点![]() (点
(点![]() 不与点
不与点![]() 重合) .当
重合) .当![]() 时,请直接写出
时,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() (0,1),点
(0,1),点![]() (1,0),正方形
(1,0),正方形![]() 的两条对角线的交点为
的两条对角线的交点为![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() .延长
.延长![]() 至点
至点![]() ,使
,使![]() ,以
,以![]() ,
,![]() 为邻边做正方形
为邻边做正方形![]() .
.
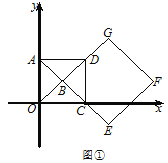
(Ⅰ)如图①,求![]() 的长及
的长及![]() 的值;
的值;
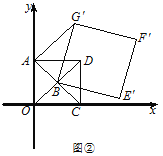
(Ⅱ)如图②,正方形![]() 固定,将正方形
固定,将正方形![]() 绕点
绕点![]() 逆时针旋转,得正方形
逆时针旋转,得正方形![]() ,记旋转角为
,记旋转角为![]() (0°<
(0°<![]() <360°),连接
<360°),连接![]() .
.
①旋转过程中,当![]() 90°时,求
90°时,求![]() 的大小;
的大小;
②在旋转过程中,求![]() 的长取最大值时,点
的长取最大值时,点![]() 的坐标及此时
的坐标及此时![]() 的大小(直接写出结果即可).
的大小(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
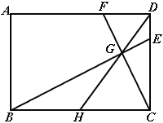
【题目】如图,在矩形ABCD中,点H为边BC的中点,点G为线段DH上一点,且∠BGC=90°,延长BG交CD于点E,延长CG交AD于点F,当CD=4,DE=1时,则DF的长为( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com