
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②P点坐标(
;②P点坐标(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,2 )(
,2 )(![]() ,2 )
,2 )
【解析】
(1)利用直线解析式求出点A、B的坐标,再利用待定系数法求二次函数解析式即可;
(2)作PF∥BO交AB于点F,证△PFD∽△OBD,得比例线段![]() ,则PF取最大值时,求得
,则PF取最大值时,求得![]() 的最大值;
的最大值;
(3)(i)点F在y轴上时,过点P作PH⊥x轴于H,根据正方形的性质可证明△CPH≌△FCO,根据全等三角形对应边相等可得PH=CO=2,然后利用二次函数解析式求解即可;(ii)点E在y轴上时,过点PK⊥x轴于K,作PS⊥y轴于S,同理可证得△EPS≌△CPK,可得PS=PK,则P点的横纵坐标互为相反数,可求出P点坐标;点E在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,同理可证得△PEN≌△PCM,可得PN=PM,则P点的横纵坐标相等,可求出P点坐标.
解:(1)直线y=x+4与坐标轴交于A、B两点,
当x=0时,y=4,x=﹣4时,y=0,
∴A(﹣4,0),B(0,4),
把A,B两点的坐标代入解析式得,![]() ,解得,
,解得,![]() ,
,
∴抛物线的解析式为![]() ;
;
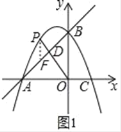
(2)①如图1,作PF∥BO交AB于点F,
∴△PFD∽△OBD,
∴![]() ,
,
∵OB为定值,
∴当PF取最大值时,![]() 有最大值,
有最大值,
设P(x,![]() ),其中﹣4<x<0,则F(x,x+4),
),其中﹣4<x<0,则F(x,x+4),
∴PF=![]() =
=![]() ,
,
∵![]() 且对称轴是直线x=﹣2,
且对称轴是直线x=﹣2,
∴当x=﹣2时,PF有最大值,
此时PF=2,![]()
![]() ;
;
②∵点C(2,0),
∴CO=2,
(i)如图2,点F在y轴上时,过点P作PH⊥x轴于H,
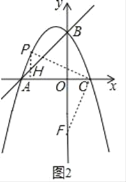
在正方形CPEF中,CP=CF,∠PCF=90°,
∵∠PCH+∠OCF=90°,∠PCH+∠HPC=90°,
∴∠HPC=∠OCF,
在△CPH和△FCO中, ,
,
∴△CPH≌△FCO(AAS),
∴PH=CO=2,
∴点P的纵坐标为2,
∴![]() ,
,
解得,![]() ,
,
∴![]() ,
,![]() ,
,
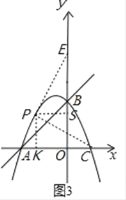
(ii)如图3,点E在y轴上时,过点PK⊥x轴于K,作PS⊥y轴于S,
同理可证得△EPS≌△CPK,
∴PS=PK,
∴P点的横纵坐标互为相反数,
∴![]() ,
,
解得x=2![]() (舍去),x=﹣2
(舍去),x=﹣2![]() ,
,
∴![]() ,
,
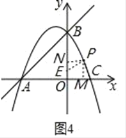
如图4,点E在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,
同理可证得△PEN≌△PCM
∴PN=PM,
∴P点的横纵坐标相等,
∴![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
∴![]() ,
,
综合以上可得P点坐标(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,2 )(
,2 )(![]() ,2 ).
,2 ).


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)(问题发现)
如图1,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,延长CA到点F,使得AF=AC,连接DF、BE,则线段BE与DF的数量关系为 ,位置关系为 ;
(2)(拓展研究)
将△ADE绕点A旋转,(1)中的结论有无变化?仅就图(2)的情形给出证明;
(3)(解决问题)
当AB=2,AD=![]() ,△ADE旋转得到D,E,F三点共线时,直接写出线段DF的长.
,△ADE旋转得到D,E,F三点共线时,直接写出线段DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子![]() 张或椅子
张或椅子![]() 把,现计划用
把,现计划用![]() 块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用
块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用![]() 块板材做椅子,用
块板材做椅子,用![]() 块板材做桌子,则下列方程组正确的是( )
块板材做桌子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划为疫情期间表现优秀的学生购买奖品.已知购买![]() 个
个![]() 奖品和
奖品和![]() 个
个![]() 奖品共需
奖品共需![]() 元;购买
元;购买![]() 个
个![]() 奖品和
奖品和![]() 个
个![]() 奖品共需
奖品共需![]() 元
元
(1)求![]() 两种奖品的单价;
两种奖品的单价;
(2)学校准备购买![]() 两种奖品共
两种奖品共![]() 个,且
个,且![]() 奖品的数量不少于
奖品的数量不少于![]() 奖品数量的一半,请设计出最省钱的购买方案,并说明理由.
奖品数量的一半,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 两点.
两点.
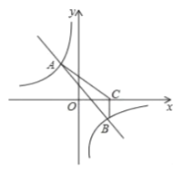
(1)求一次函数与反比例函数的解析式;
(2)根据已知条件,请直接写出不等式![]() 的解集;
的解集;
(3)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一小长假前夕,某服装店的老板到服装厂购买男士夏装和女士夏装.已知购进![]() 套男士夏装和
套男士夏装和![]() 套女士夏装需要
套女士夏装需要![]() 元;购进
元;购进![]() 套男士夏装和
套男士夏装和![]() 套女士夏装需要
套女士夏装需要![]() 元.
元.
(1)求男士夏装和女士夏装每套进价分别是多少元;
(2)若![]() 套男士夏装的售价为
套男士夏装的售价为![]() 元,
元,![]() 套女士夏装的售价为
套女士夏装的售价为![]() 元,时装店决定购进男士夏装的数量为女士夏装的数量的
元,时装店决定购进男士夏装的数量为女士夏装的数量的![]() 还多
还多![]() 套,如果购进的男士夏装和女士夏装全部售出后的总利润超过
套,如果购进的男士夏装和女士夏装全部售出后的总利润超过![]() 元,那么此次至少可购进多少套女士夏装?
元,那么此次至少可购进多少套女士夏装?
查看答案和解析>>
科目:初中数学 来源: 题型:
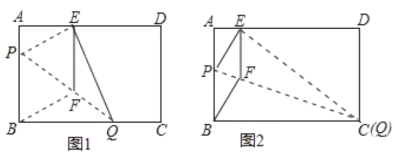
【题目】如图1,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() 也随之移动;
也随之移动;
①当点![]() 与点
与点![]() 重合时(如图2),求菱形
重合时(如图2),求菱形![]() 的边长;
的边长;
②若限定![]() 分别在边
分别在边![]() 上移动,求出点
上移动,求出点![]() 在边
在边![]() 上移动的最大距离.
上移动的最大距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
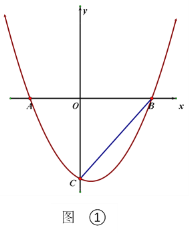
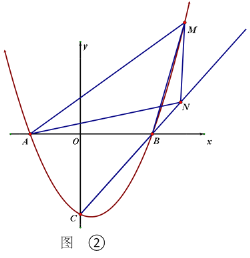
【题目】如图,抛物线![]() 交x轴于A、B两点(点A在点B的左侧),
交x轴于A、B两点(点A在点B的左侧),![]() .
.
(1)求抛物线的函数表达式;
(2)如图①,连接BC,点P在抛物线上,且∠BCO=![]() ∠PBA.求点P的坐标
∠PBA.求点P的坐标
(3)如图②,M是抛物线上一点,N为射线CB上的一点,且M、N两点均在第一象限内,B、N是位于直线AM同侧的不同两点,![]() ,点M到
,点M到![]() 轴的距离为2L,△AMN的面积为5L,且∠ANB=∠MBN,请问MN的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
轴的距离为2L,△AMN的面积为5L,且∠ANB=∠MBN,请问MN的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com