
【题目】(1)(问题发现)
如图1,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,延长CA到点F,使得AF=AC,连接DF、BE,则线段BE与DF的数量关系为 ,位置关系为 ;
(2)(拓展研究)
将△ADE绕点A旋转,(1)中的结论有无变化?仅就图(2)的情形给出证明;
(3)(解决问题)
当AB=2,AD=![]() ,△ADE旋转得到D,E,F三点共线时,直接写出线段DF的长.
,△ADE旋转得到D,E,F三点共线时,直接写出线段DF的长.

【答案】(1)DF=BE,DF⊥BE;(2)详见解析;(3)DF=![]() +1或
+1或![]() ﹣1
﹣1
【解析】
(1)通过证明△ABE≌△AFD,可得DF=BE,DF⊥BE;
(2)通过证明△ADF≌△AEB,可得DF=BE,DF⊥BE;
(3)分点D在AB左侧和右侧两种情况讨论,由等腰直角三角形的性质和勾股定理可求FH的长,即可求DF的长.
(1)延长FD交BE于点M
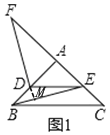
∵△ABC和△ADE都是等腰直角三角形
∴AD=AE,AB=AC,∠BAC=90°=∠FAD
∵AF=AC
∴AF=AB,且AD=AE,∠BAE=∠DAF=90°
∴△ABE≌△AFD(SAS)
∴FD=BE,∠F=∠ABE,
∵∠ABE+∠AEB=90°
∴∠F+∠AEB=90°
∴∠FME=90°
∴FD⊥BE
故答案为:DF=BE,DF⊥BE
【拓展研究】
(2)

∵∠BAC=90°=∠EAD
∴∠DAF=∠EAB=90°+∠EAF
在△ADF 和△AEB 中
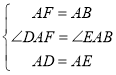
∴△ADF≌△AEB
DF=BE,∠F=∠EBA
设 CF 和 BE 相交于点 H,则∠EHF=∠CHB
∵∠BAC=∠DAE=90°
∴∠EBA+∠CHB=90°
∴∠F+∠EHF=90°
∴DF⊥BE
(3)当点D在AB的左侧,
如图,过点A作AH⊥EF于点H,
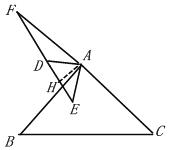
∵△ADE是等腰直角三角形,AD=AE=![]() ,AH⊥EF
,AH⊥EF
∴DE=2,AH=DH=![]() DE=1
DE=1
∵FH=![]() =
=![]()
∴FD=FH﹣DH=![]() ﹣1
﹣1
当点D在AB右侧,
如图,过点A作AH⊥EF于点H,
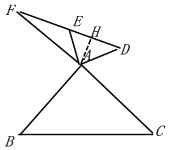
同理可求:FH=![]()
∴FD=FH+HD=![]() +1
+1
综上所述:DF=![]() +1或
+1或![]() ﹣1
﹣1


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】2019年春节期间,兰州市开展了以“精致兰州志愿同行”为主题的系列志愿服务活动.金老师和程老师积极参加志愿者活动,当时有下列四个志愿者工作岗位供他们选择:
①“送温暖”活动岗位:为困难家庭打扫卫生,为留守儿童提供学业辅导;(分别用![]() ,
,![]() 表示)
表示)
②“送平安”活动岗位:消防安全常识宣传,人员密集场所维护秩序.(分别用![]() ,
,![]() 表示)
表示)
(1)金老师从四个岗位中随机选取一个报名,恰好选择“送温暖”活动岗位的概率是多少?
(2)若金老师和程老师各随机从四个活动岗位中选一个报名,请用树状图或列表法求出他们恰好都选择同一个岗位的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社的一则广告如下:

甲公司想分批组织员工到延安红色旅游学习.
(1)如果第一批组织40人去学习,则公司应向旅行社交费 元;
(2)如果公司计划用29250元组织第一批员工去学习,问这次旅游学习应安排多少人参加?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意两点P1(x1,y1),P2(x2,y2),如果![]() ,则称P1与P2互为“d-距点”.例如:点P1(3,6),点P2(1,7),由d=|3-1|+|6-7|=3,可得点P1与P2互为“3-距点”.
,则称P1与P2互为“d-距点”.例如:点P1(3,6),点P2(1,7),由d=|3-1|+|6-7|=3,可得点P1与P2互为“3-距点”.
(1)在点D(-2,-2),E(5,-1),F(0,4)中,原点O的“4-距点"是____(填字母);
(2)已知点A(2,1),点B(0,b),过点B作平行于x轴的直线l.
①当b=3时,直线l上点A的“2-距点"的坐标为_______;
②若直线l上存在点A的2-距点”,求b的取值范围:
(3)已知点M(1,2),N(3,2),C(m,0),⊙C的半径为![]() ,若在线段MN上存在点P,在⊙C上存在点Q,使得点P与点Q互为“5-距点",直接写出m的取值范围.
,若在线段MN上存在点P,在⊙C上存在点Q,使得点P与点Q互为“5-距点",直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解七年级学生身体发育状况,学校抽取一部分学生测量身高(单位:m),绘制处如下的统计图①和图②.请根据相关信息,解答下列问题:
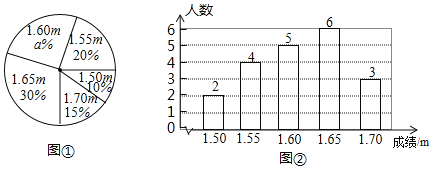
(1)图①中a的值为 ;
(2)求统计的这组学生身高数据的平均数、众数和中位数;
(3)如果全校七年级学生有300人,那么估计身高大于1.65m的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 网格的每个小正方形边长均为1,每个小正方形的顶点称为格点.已知
网格的每个小正方形边长均为1,每个小正方形的顶点称为格点.已知![]() 和
和![]() 的顶点都在格点上,线段
的顶点都在格点上,线段![]() 的中点为
的中点为![]() .
.
(1)以点![]() 为旋转中心,分别画出把
为旋转中心,分别画出把![]() 顺时针旋转
顺时针旋转![]() ,
,![]() 后的
后的![]() ,
,![]() ;
;
(2)利用(1)变换后所形成的图案,解答下列问题:
①直接写出四边形![]() ,四边形
,四边形![]() 的形状;
的形状;
②直接写出 的值;
的值;
③设![]() 的三边
的三边![]() ,
,![]() ,
,![]() ,请证明勾股定理.
,请证明勾股定理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市青少年宫准备在七月一日组织市区部分学校的中小学生到本市A,B,C,D,E五个红色旅游景区“一日游”,每名学生只能在五个景区中任选一个.为估算到各景区旅游的人数,青少年宫随机抽取这些学校的部分学生,进行了“五个红色景区,你最想去哪里”的问卷调查,在统计了所有的调查问卷后将结果绘制成如图所示的统计图.
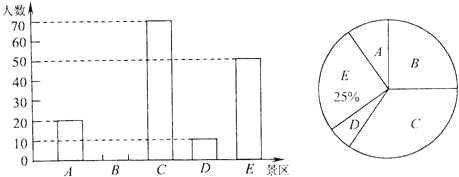
(1)求参加问卷调查的学生数,并将条形统计图补充完整;
(2)若参加“一日游”的学生为1000人,请估计到C景区旅游的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com