
ЎѕМвДїЎї2019ДкґєЅЪЖЪјдЈ¬АјЦЭКРїЄХ№БЛТФЎ°ѕ«ЦВАјЦЭЦѕФёН¬РРЎ±ОЄЦчМвµДПµБРЦѕФё·юОс»о¶Ї.ЅрАПК¦єНіМАПК¦»эј«ІОјУЦѕФёХЯ»о¶ЇЈ¬µ±К±УРПВБРЛДёцЦѕФёХЯ№¤ЧчёЪО»№©ЛыГЗСЎФсЈє
ўЩЎ°ЛНОВЕЇЎ±»о¶ЇёЪО»ЈєОЄА§ДСјТНҐґтЙЁОАЙъЈ¬ОЄБфКШ¶щНЇМṩѧҵёЁµјЈ»ЈЁ·Ц±рУГ![]() Ј¬
Ј¬![]() ±нКѕЈ©
±нКѕЈ©
ўЪЎ°ЛНЖЅ°ІЎ±»о¶ЇёЪО»ЈєПы·А°ІИ«іЈК¶Рыґ«Ј¬ИЛФ±ГЬјЇіЎЛщО¬»¤ЦИРт.ЈЁ·Ц±рУГ![]() Ј¬
Ј¬![]() ±нКѕЈ©
±нКѕЈ©
ЈЁ1Ј©ЅрАПК¦ґУЛДёцёЪО»ЦРЛж»ъСЎИЎТ»ёц±ЁГыЈ¬ЗЎєГСЎФсЎ°ЛНОВЕЇЎ±»о¶ЇёЪО»µДёЕВККЗ¶аЙЩЈї
ЈЁ2Ј©ИфЅрАПК¦єНіМАПК¦ёчЛж»ъґУЛДёц»о¶ЇёЪО»ЦРСЎТ»ёц±ЁГыЈ¬ЗлУГКчЧґНј»тБР±н·ЁЗуіцЛыГЗЗЎєГ¶јСЎФсН¬Т»ёцёЪО»µДёЕВК.
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј»ЈЁ2Ј©
Ј»ЈЁ2Ј©![]()
ЎѕЅвОцЎї
ЈЁ1Ј©Ц±ЅУАыУГёЕВК№«КЅЗуЅвјґїЙЈ»
ЈЁ2Ј©ёщѕЭМвТвПИ»іцКчЧґНјЈ¬µГіцЛщУРµИїЙДЬµДЅб№ыКэЈ¬ФЩХТіцЛыГЗЗЎєГ¶јСЎФсН¬Т»ёЪО»µДЅб№ыКэЈ¬И»єуёщѕЭёЕВК№«КЅЗуЅвјґїЙЈ®
ЅвЈєЈЁ1Ј©ЅрАПК¦СЎФсЎ°ЛНОВЕЇЎ±»о¶ЇёЪО»µДёЕВКОЄЈє![]() Ј»
Ј»
ЈЁ2Ј©БР±нИзПВЈє
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
»тКчЧґНјИзПВЈє
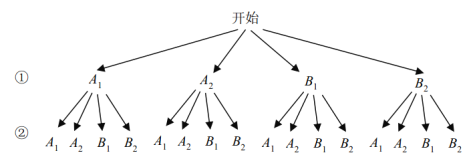
№ІУР16ЦЦµИїЙДЬµДЅб№ыКэЈ¬ЅрАПК¦єНіМАПК¦ЗЎєГСЎФсН¬Т»»о¶ЇёЪО»µДЅб№ыКэОЄ4Ј¬
ЛщТФЛыГЗЗЎєГСЎФсН¬Т»»о¶ЇёЪО»µДёЕВКЈє![]() .
.


 Т»ПЯГыК¦ИЁНюЧчТµ±ѕПµБРґр°ё
Т»ПЯГыК¦ИЁНюЧчТµ±ѕПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄ¶юґОєЇКэyЈЅЈЁx©ЃmЈ©2+2ЈЁx©ЃmЈ©ЈЁmОЄіЈКэЈ©
ЈЁ1Ј©ЗуЦ¤ЈєІ»ВЫmОЄєОЦµЈ¬ёГєЇКэµДНјПуУлxЦбЧЬУРБЅёцІ»Н¬µД№«№ІµгЈ»
ЈЁ2Ј©µ±mИЎКІГґЦµК±Ј¬ёГєЇКэµДНјПу№ШУЪyЦб¶ФіЖЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНј1ЈЁЧўЈєУлНј2НкИ«ПаН¬Ј©Ј¬ФЪЦ±ЅЗЧш±кПµЦРЈ¬ЕЧОпПЯѕ№эµгИэµг![]() ,
,![]() ,
,![]() Ј®
Ј®
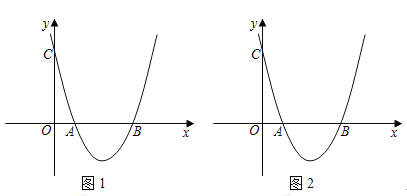
ЈЁ1Ј©ЗуЕЧОпПЯµДЅвОцКЅєН¶ФіЖЦбЈ»
ЈЁ2Ј©![]() КЗЕЧОпПЯ¶ФіЖЦбЙПµДТ»µгЈ¬ЗуВъЧг
КЗЕЧОпПЯ¶ФіЖЦбЙПµДТ»µгЈ¬ЗуВъЧг![]() µДЦµОЄЧоРЎµДµг
µДЦµОЄЧоРЎµДµг![]() Чш±кЈЁЗлФЪНј1ЦРМЅЛчЈ©Ј»
Чш±кЈЁЗлФЪНј1ЦРМЅЛчЈ©Ј»
ЈЁ3Ј©ФЪµЪЛДПуПЮµДЕЧОпПЯЙПКЗ·сґжФЪµг![]() Ј¬К№ЛД±ЯРО
Ј¬К№ЛД±ЯРО![]() КЗТФ
КЗТФ![]() ОЄ¶ФЅЗПЯЗТГж»эОЄ
ОЄ¶ФЅЗПЯЗТГж»эОЄ![]() µДЖЅРРЛД±ЯРОЈїИфґжФЪЈ¬ЗлЗуіцµг
µДЖЅРРЛД±ЯРОЈїИфґжФЪЈ¬ЗлЗуіцµг![]() Чш±кЈ¬ИфІ»ґжФЪЗлЛµГчАнУЙ.ЈЁЗлФЪНј2ЦРМЅЛчЈ©
Чш±кЈ¬ИфІ»ґжФЪЗлЛµГчАнУЙ.ЈЁЗлФЪНј2ЦРМЅЛчЈ©
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµ![]() ЦРЈ¬ЕЧОпПЯ
ЦРЈ¬ЕЧОпПЯ![]()
ЈЁ1Ј©µ±![]() К±Ј¬ЗуЕЧОпПЯ
К±Ј¬ЗуЕЧОпПЯ![]() µД¶ҐµгЧш±кЈ»
µД¶ҐµгЧш±кЈ»
ЈЁ2Ј©ТСЦЄµг![]() Ј¬ЕЧОпПЯ
Ј¬ЕЧОпПЯ![]() Ул
Ул![]() ЦбЅ»УЪµг
ЦбЅ»УЪµг![]() ЈЁІ»Ул
ЈЁІ»Ул![]() ЦШєПЈ©Ј¬Ѕ«µг
ЦШєПЈ©Ј¬Ѕ«µг![]() ИЖµг
ИЖµг![]() ДжК±ХлРэЧЄ90ЎгЦБµг
ДжК±ХлРэЧЄ90ЎгЦБµг![]() Ј¬
Ј¬
ўЩЦ±ЅУРґіцµг![]() µДЧш±кЈЁУГє¬
µДЧш±кЈЁУГє¬![]() µДґъКэКЅ±нКѕЈ©Ј»
µДґъКэКЅ±нКѕЈ©Ј»
ўЪИфЕЧОпПЯ![]() УлПЯ¶О
УлПЯ¶О![]() УРЗТЅцУРТ»ёц№«№ІµгЈ¬Зу
УРЗТЅцУРТ»ёц№«№ІµгЈ¬Зу![]() µДИЎЦµ·¶О§Ј®
µДИЎЦµ·¶О§Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµ![]() ЦРЈ¬ТСЦЄЕЧОпПЯ
ЦРЈ¬ТСЦЄЕЧОпПЯ![]() .
.
(1)ЗуЕЧОпПЯµД¶ФіЖЦб(УГє¬![]() µДКЅЧУИҐ±нКѕ)Ј»
µДКЅЧУИҐ±нКѕ)Ј»
(2)Ифµг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ¶јФЪЕЧОпПЯ
¶јФЪЕЧОпПЯ![]() ЙПЈ¬Фт
ЙПЈ¬Фт![]() Ўў
Ўў![]() Ўў
Ўў![]() µДґуРЎ№ШПµОЄ_______Ј»
µДґуРЎ№ШПµОЄ_______Ј»
(3)Ц±ПЯ![]() Ул
Ул![]() ЦбЅ»УЪµг
ЦбЅ»УЪµг![]() Ј¬Ул
Ј¬Ул![]() ЦбЅ»УЪµг
ЦбЅ»УЪµг![]() Ј¬№эµг
Ј¬№эµг![]() Ччґ№Ц±УЪ
Ччґ№Ц±УЪ![]() ЦбµДЦ±ПЯ
ЦбµДЦ±ПЯ![]() УлЕЧОпПЯ
УлЕЧОпПЯ![]() УРБЅёцЅ»µгЈ¬ФЪЕЧОпПЯ¶ФіЖЦбУТІаµДµгјЗОЄ
УРБЅёцЅ»µгЈ¬ФЪЕЧОпПЯ¶ФіЖЦбУТІаµДµгјЗОЄ![]() Ј¬µ±
Ј¬µ±![]() ОЄ¶ЫЅЗИэЅЗРОК±Ј¬Зу
ОЄ¶ЫЅЗИэЅЗРОК±Ј¬Зу![]() µДИЎЦµ·¶О§Ј®
µДИЎЦµ·¶О§Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
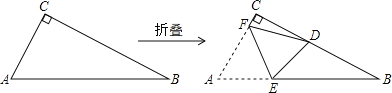
ЎѕМвДїЎїИзНјЈ¬ЎчABCЦРЈ¬ЎПACBЈЅ90ЎгЈ¬ACЎЬBCЈ¬Ѕ«ЎчABCСШEFХЫµюЈ¬К№µгAВдФЪЦ±ЅЗ±ЯBCЙПµДDµгґ¦Ј¬ЙиEFУлABЎўAC±Я·Ц±рЅ»УЪµгEЎўµгFЈ¬Из№ыХЫµюєуЎчCDFУлЎчBDEѕщОЄµИСьИэЅЗРОЈ¬ДЗГґЎПBЈЅ_____Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
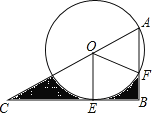
ЎѕМвДїЎїИзНјЈ¬RtЎчABCЈ¬ЎПB=90ЎгЈ¬ЎПC=30ЎгЈ¬OОЄACЙПТ»µгЈ¬OA=2Ј¬ТФOОЄФІРДЈ¬ТФOAОЄ°лѕ¶µДФІУлCBПаЗРУЪµгEЈ¬УлABПаЅ»УЪµгFЈ¬Б¬ЅУOEЎўOFЈ¬ФтНјЦРТхУ°Ії·ЦµДГж»эКЗ_______Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДі№¤і§УР20Гы№¤ИЛЈ¬ГїИЛГїМмјУ№¤јЧЦЦБгјю5ёц»тТТЦЦБгјю4ёцЈ®ФЪХв20Гы№¤ИЛµ±ЦРЈ¬ЕЙxИЛјУ№¤јЧЦЦБгјюЈ¬ЖдУаµДјУ№¤ТТЦЦБгјюЈ¬ТСЦЄГїјУ№¤Т»ёцјЧЦЦБгјюїЙ»сАы16ФЄЈ¬ГїјУ№¤Т»ёцТТЦЦБгјюїЙТФ»сАы24ФЄЈ®
ЈЁ1Ј©РґіцґЛ№¤і§ГїМмЛщ»сАыИуyЈЁФЄЈ©УлxЈЁИЛЈ©Ц®јдµДєЇКэ№ШПµКЅЈЁЦ»РґіцЅвОцКЅЈ©
ЈЁ2Ј©ИфТЄК№№¤і§ГїМм»сАыІ»µНУЪ1800ФЄЈ¬ОКЦБЙЩТЄЕЙ¶аЙЩИЛјУ№¤ТТЦЦБгјю?
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЈЁ1Ј©ЈЁОКМв·ўПЦЈ©
ИзНј1Ј¬ЎчABCєНЎчADE¶јКЗµИСьЦ±ЅЗИэЅЗРОЈ¬ЎПBACЈЅЎПDAEЈЅ90ЎгЈ¬СУі¤CAµЅµгFЈ¬К№µГAFЈЅACЈ¬Б¬ЅУDFЎўBEЈ¬ФтПЯ¶ОBEУлDFµДКэБї№ШПµОЄЎЎ ЎЎЈ¬О»ЦГ№ШПµОЄЎЎ ЎЎЈ»
ЈЁ2Ј©ЈЁНШХ№СРѕїЈ©
Ѕ«ЎчADEИЖµгAРэЧЄЈ¬ЈЁ1Ј©ЦРµДЅбВЫУРОЮ±д»ЇЈїЅцѕННјЈЁ2Ј©µДЗйРОёшіцЦ¤ГчЈ»
ЈЁ3Ј©ЈЁЅвѕцОКМвЈ©
µ±ABЈЅ2Ј¬ADЈЅ![]() Ј¬ЎчADEРэЧЄµГµЅDЈ¬EЈ¬FИэµг№ІПЯК±Ј¬Ц±ЅУРґіцПЯ¶ОDFµДі¤Ј®
Ј¬ЎчADEРэЧЄµГµЅDЈ¬EЈ¬FИэµг№ІПЯК±Ј¬Ц±ЅУРґіцПЯ¶ОDFµДі¤Ј®

Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com