
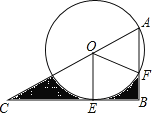
【题目】如图,Rt△ABC,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,以OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE、OF,则图中阴影部分的面积是_______.
科目:初中数学 来源: 题型:
【题目】如图,数轴上的点A、B、C、D、E表示连续的五个整数,对应的数分别为a、b、c、d、e。
(1)若a+e=0,直接写出代数式b+c+d的值为_____;
(2)若a+b=7,先化简,再求值:![]() ;
;
(3)若a+b+c+d+e=5,数轴上的点M表示的实数为m,且满足MA+ME>12,则m的范围是____。
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x+b与双曲线y=![]() 的一个交点为A(2,4),与y轴交于点B.
的一个交点为A(2,4),与y轴交于点B.
(1)求m的值和点B的坐标;
(2)点P在双曲线y=![]() 上,△OBP的面积为8,直接写出点P的坐标.
上,△OBP的面积为8,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年春节期间,兰州市开展了以“精致兰州志愿同行”为主题的系列志愿服务活动.金老师和程老师积极参加志愿者活动,当时有下列四个志愿者工作岗位供他们选择:
①“送温暖”活动岗位:为困难家庭打扫卫生,为留守儿童提供学业辅导;(分别用![]() ,
,![]() 表示)
表示)
②“送平安”活动岗位:消防安全常识宣传,人员密集场所维护秩序.(分别用![]() ,
,![]() 表示)
表示)
(1)金老师从四个岗位中随机选取一个报名,恰好选择“送温暖”活动岗位的概率是多少?
(2)若金老师和程老师各随机从四个活动岗位中选一个报名,请用树状图或列表法求出他们恰好都选择同一个岗位的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下:如图,两侧最长斜拉索![]() ,
,![]() 相交于点
相交于点![]() ,分别与桥面交于
,分别与桥面交于![]() ,
,![]() 两点,且点
两点,且点![]() ,
,![]() ,
,![]() 在同一竖直平面内.测得
在同一竖直平面内.测得![]() ,
,![]() ,
,![]() 米,请帮助该小组根据测量数据,求斜拉索顶端点
米,请帮助该小组根据测量数据,求斜拉索顶端点![]() 到
到![]() 的距离.(参考数据:
的距离.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
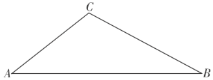
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社的一则广告如下:

甲公司想分批组织员工到延安红色旅游学习.
(1)如果第一批组织40人去学习,则公司应向旅行社交费 元;
(2)如果公司计划用29250元组织第一批员工去学习,问这次旅游学习应安排多少人参加?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com