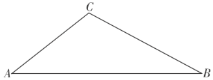
【题目】某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动，他们制订了测量方案，并利用课余时间借助该桥斜拉索完成了实地测量．测量结果如下：如图，两侧最长斜拉索
，
相交于点
，分别与桥面交于
，
两点，且点，，在同一竖直平面内．测得
，
，
米，请帮助该小组根据测量数据，求斜拉索顶端点到
的距离．（参考数据：
，
，
，
，
，
．）
科目：初中数学 来源： 题型：
【题目】抛物线
的对称轴为直线
，图象过
点，部分图象如图所示，下列判断：①
；②
；③
；④若点
，
均在抛物线上，则
，其中正确的个数是（ ）
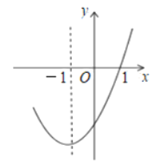
A.1B.2C.3D.4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知抛物线
.
(1)求抛物线的对称轴(用含
的式子去表示)；
(2)若点
，
，
都在抛物线上，则
、
、
的大小关系为_______；
(3)直线
与
轴交于点
，与
轴交于点
，过点作垂直于轴的直线
与抛物线有两个交点，在抛物线对称轴右侧的点记为
，当
为钝角三角形时，求的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
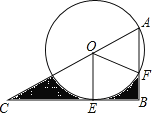
【题目】如图，Rt△ABC，∠B=90°，∠C=30°，O为AC上一点，OA=2，以O为圆心，以OA为半径的圆与CB相切于点E，与AB相交于点F，连接OE、OF，则图中阴影部分的面积是_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
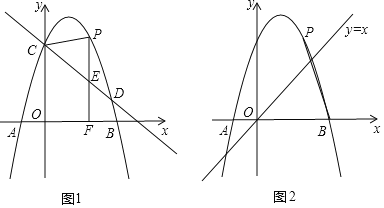
【题目】如图1所示，抛物线
与
轴交于点
两点，与
轴交于点
，直线
经过点
，与抛物线另一个交点为，点
是抛物线上的一个动点，过点作
轴于点
，交直线
于点
（1）求抛物线的解析式
（2）当点在直线上方，且
是以
为腰的等腰三角形时，求的坐标
（3）如图2所示，若点为对称轴右侧抛物线上一点，连接
，以为直角顶点，线段为较长直角边，构造两直角边比为
的
，是否存在点，使点
恰好落在直线
上？若存在，请直接写出相应点的横坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工厂有20名工人，每人每天加工甲种零件5个或乙种零件4个．在这20名工人当中，派x人加工甲种零件，其余的加工乙种零件，已知每加工一个甲种零件可获利16元，每加工一个乙种零件可以获利24元．
（1）写出此工厂每天所获利润y（元）与x（人）之间的函数关系式（只写出解析式）
（2）若要使工厂每天获利不低于1800元，问至少要派多少人加工乙种零件?
查看答案和解析>>
科目：初中数学 来源： 题型：
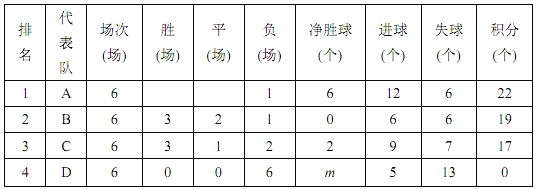
【题目】2018年9月17日世界人工智能大会在．上海召开，人工智能的变革力在教育、制造等领域加速落地．在某市举办的一次中学生机器人足球赛中，有四个代表队进入决赛，决赛中，每个队分别与其它三个队进行主客场比赛各一场(即每个队要进行6场比赛)，以下是积分表的一-部分．
(说明：积分=胜场积分十平场积分+负场积分)
（1）D代表队的净胜球数m=______；
（2）本次决赛中，胜一场积______分，平一场积______分，负一场积_______分；
（3）此次竞赛的奖金分配方案为：进入决赛的每支代表队都可以获得参赛奖金6000元；另外，在决赛期间，每胜一场可以再获得奖金2000元，每平一场再获得奖金1000元．请根据表格提供的信息，求出冠军A队一共能获得多少奖金．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题提出
（1）如图①，在矩形ABCD中，AB=2AD，E为CD的中点，则∠AEB ∠ACB（填“＞”“＜”“=”）；
问题探究
（2）如图②，在正方形ABCD中，P为CD边上的一个动点，当点P位于何处时，∠APB最大？并说明理由；
问题解决
（3）如图③，在一幢大楼AD上装有一块矩形广告牌，其侧面上、下边沿相距6米（即AB=6米），下边沿到地面的距离BD=11.6米．如果小刚的睛睛距离地面的高度EF为1.6米，他从远处正对广告牌走近时，在P处看广告效果最好（视角最大），请你在图③中找到点P的位置，并计算此时小刚与大楼AD之间的距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
