
【题目】问题提出
(1)如图①,在矩形ABCD中,AB=2AD,E为CD的中点,则∠AEB ∠ACB(填“>”“<”“=”);
问题探究
(2)如图②,在正方形ABCD中,P为CD边上的一个动点,当点P位于何处时,∠APB最大?并说明理由;
问题解决
(3)如图③,在一幢大楼AD上装有一块矩形广告牌,其侧面上、下边沿相距6米(即AB=6米),下边沿到地面的距离BD=11.6米.如果小刚的睛睛距离地面的高度EF为1.6米,他从远处正对广告牌走近时,在P处看广告效果最好(视角最大),请你在图③中找到点P的位置,并计算此时小刚与大楼AD之间的距离.

【答案】(1)>;(2)当点P位于CD的中点时,∠APB最大,理由见解析;(3)4![]() 米.
米.
【解析】
(1)过点E作EF⊥AB于点F,由矩形的性质和等腰三角形的判定得到:△AEF是等腰直角三角形,易证∠AEB=90°,而∠ACB<90°,由此可以比较∠AEB与∠ACB的大小
(2)假设P为CD的中点,作△APB的外接圆⊙O,则此时CD切⊙O于P,在CD上取任意异于P点的点E,连接AE,与⊙O交于点F,连接BE、BF;由∠AFB是△EFB的外角,得∠AFB>∠AEB,且∠AFB与∠APB均为⊙O中弧AB所对的角,则∠AFB=∠APB,即可判断∠APB与∠AEB的大小关系,即可得点P位于何处时,∠APB最大;
(3)过点E作CE∥DF,交AD于点C,作AB的垂直平分线,垂足为点Q,并在垂直平分线上取点O,使OA=CQ,以点O为圆心,OB为半径作圆,则⊙O切CE于点G,连接OG,并延长交DF于点P,连接OA,再利用勾股定理以及长度关系即可得解.
解:(1)∠AEB>∠ACB,理由如下:
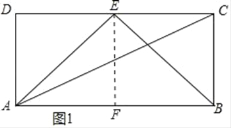
如图1,过点E作EF⊥AB于点F,
∵在矩形ABCD中,AB=2AD,E为CD中点,
∴四边形ADEF是正方形,
∴∠AEF=45°,
同理,∠BEF=45°,
∴∠AEB=90°.
而在直角△ABC中,∠ABC=90°,
∴∠ACB<90°,
∴∠AEB>∠ACB.
故答案为:>;
(2)当点P位于CD的中点时,∠APB最大,理由如下:
假设P为CD的中点,如图2,作△APB的外接圆⊙O,则此时CD切⊙O于点P,
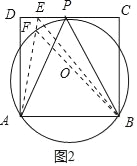
在CD上取任意异于P点的点E,连接AE,与⊙O交于点F,连接BE,BF,
∵∠AFB是△EFB的外角,
∴∠AFB>∠AEB,
∵∠AFB=∠APB,
∴∠APB>∠AEB,
故点P位于CD的中点时,∠APB最大:
(3)如图3,过点E作CE∥DF交AD于点C,作线段AB的垂直平分线,垂足为点Q,并在垂直平分线上取点O,使OA=CQ,
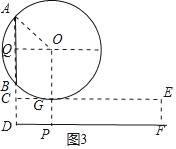
以点O为圆心,OA长为半径作圆,则⊙O切CE于点G,连接OG,并延长交DF于点P,此时点P即为小刚所站的位置,
由题意知DP=OQ=![]() ,
,
∵OA=CQ=BD+QB﹣CD=BD+![]() AB﹣CD,
AB﹣CD,
BD=11.6米,![]() AB=3米,CD=EF=1.6米,
AB=3米,CD=EF=1.6米,
∴OA=11.6+3﹣1.6=13米,
∴DP=![]() 米,
米,
即小刚与大楼AD之间的距离为4![]() 米时看广告牌效果最好.
米时看广告牌效果最好.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E为BC上的点,AD平分∠BAE,CA=CD.
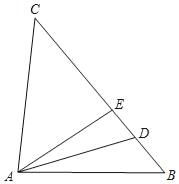
(1)求证:∠CAE=∠B;
(2)若∠B=50°,∠C=3∠DAB,求∠C的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(3,-2)在反比例函数y=![]() 的图象上,则下列点也在该反比例函数y=
的图象上,则下列点也在该反比例函数y=![]() 的图象的是( )
的图象的是( )
A. (3,-3) B. (1,6) C. (-2,3) D. (-2,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
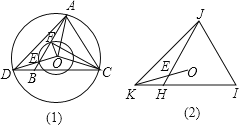
【题目】观察发现:如图(1),⊙O是△ADC的外接圆,点B是边CD上的一点,且△ABC是等边三角形.OD与AB交于点E,以O为圆心、OE为半径的圆交AB于点F,连接CF、OF.
(1)求∠AOD的度数;
(2)线段AE、CF有何大小关系?证明你的猜想.
拓展应用:如图(2),△HJI是等边三角形,点K是IH延长线上的一点.点O是△JKI的外接圆圆心,OK与JH相交于点E.如果等边三角形△JHI的边长为2,请直接写出JE的最小值和此时∠JEO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,小丽一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
租车公司:按日收取固定租金80元,另外再按租车时间计费.
共享汽车:无固定租金,直接以租车时间(时)计费.
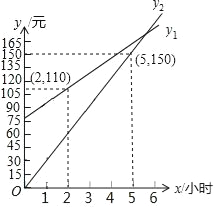
如图是两种租车方式所需费用y1(元)、y2(元)与租车时间x(时)之间的函数图象,根据以上信息,回答下列问题:
(1)分别求出y1、y2与x的函数表达式;
(2)请你帮助小丽一家选择合算的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
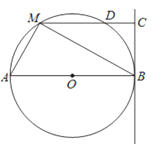
【题目】如图,直线BC与半径为6的⊙O相切于点B,点M是圆上的动点,过点M作MC⊥BC,垂足为C,MC与⊙O交于点D,AB为⊙O的直径,连接MA、MB,设MC的长为x,(6<x<12).
(1)当x=9时,求BM的长和△ABM的面积;
(2)是否存在点M,使MDDC=20?若存在,请求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )

A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
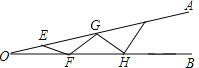
【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH,添的钢管长度都与OE相等,则最多能添加这样的钢管_____根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com