
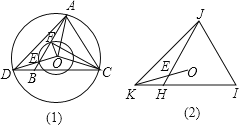
����Ŀ���۲췢�֣���ͼ��1������O����ADC�����Բ����B�DZ�CD�ϵ�һ�㣬����ABC�ǵȱ������Σ�OD��AB���ڵ�E����OΪԲ�ġ�OEΪ�뾶��Բ��AB�ڵ�F������CF��OF��
��1������AOD�Ķ�����
��2���߶�AE��CF�кδ�С��ϵ��֤����IJ��룮
��չӦ�ã���ͼ��2������HJI�ǵȱ������Σ���K��IH�ӳ����ϵ�һ�㣮��O����JKI�����ԲԲ�ģ�OK��JH�ཻ�ڵ�E������ȱ���������JHI�ı߳�Ϊ2����ֱ��д��JE����Сֵ�ʹ�ʱ��JEO�Ķ�����
���𰸡��۲췢������1����AOD=120�㣻��2��������AE=CF�����ɼ���������չӦ�ã� JE����СֵΪ![]() ����ʱ��JEO=45�㣮
����ʱ��JEO=45�㣮
��������
�۲췢�֣���1������Բ�ܽǶ������ɽ�����⣻
��2�����ۣ�AE=CF����취֤����AOE�ա�COF���ɣ�
��չӦ�ã���OΪԲ�ģ���OE��Ϊ�뾶��Բ����JH��F������IF���������Ͻ��ۿɵã�JE=IF�����ݴ��߶���̼��ɽ�����⣻
�⣺
�۲췢�֣���1���ߡ�ABC�ǵȱ������Σ�
���ACB=60�㣬
���AOD=2��ACB=120��
��2�����ۣ�AE=CF��
�������£��ߡ�AOD=120�㣬
���OEF+��OAF=60�㣬
�ߡ�OAC+��OAF=60�㣬
���OEF=��OAC��
��OE=OF��OA=OC��
���OEF=��OFE=��OAC=��OCA��
���EOF=��AOC��
���EOF+��AOF=��AOC+��AOF��
���AOE=��COF��
���AOE�ա�COF��
��AE=CF��
��չӦ�ã���OΪԲ�ģ���OE��Ϊ�뾶��Բ����JH��F������IF���������Ͻ��ۿɵã�JE=IF��
��IF��JHʱIF��С��IF=JIsin60��=2��![]() =
=![]() ��
��
�ߡ�FJO=��OIF����FGJ=��OGI��
���JOI=��JFI=90�㣬
���OJI=45�㣬
���JEO=��OJI=45�㣬
��JE����СֵΪ![]() ����ʱ��JEO=45�㣮
����ʱ��JEO=45�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
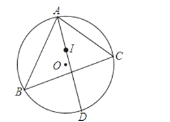
����Ŀ����IΪ��ABC�����ģ�AI���ӳ��߽���ABC�����Բ��D����DΪԲ�ģ�DIΪ�뾶�������Ƿ���B���C��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
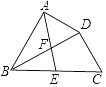
����Ŀ����ͼ�����ı���ABCD�У�BDƽ�֡�ABC����BAD=��BDC=90�㣬EΪBC���е㣬AE��BD�ཻ�ڵ�F����BC=4����CBD=30�㣬��DF�ij�Ϊ�� ��
A. ![]()
![]() B.
B. ![]()
![]() C.
C. ![]()
![]() D.
D. ![]()
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
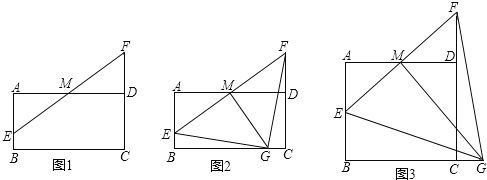
����Ŀ����ͼ���ھ���ABCD�У�AD=4��M��AD���е㣬��E���߶�AB��һ���㣬����EM���ӳ����߶�CD���ӳ����ڵ�F��
��1����ͼ1����֤��AE=DF��
��2����ͼ2������M��MG��EF���߶�BC�ڵ�G����ME=MG����֤��BE=CG��
��3����ͼ3����AB=2![]() ������M��MG��EF���߶�BC���ӳ����ڵ�G�����߶�AE���ȵ�ȡֵ��Χ��
������M��MG��EF���߶�BC���ӳ����ڵ�G�����߶�AE���ȵ�ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��̣�m-1��x2-��m-2��x+![]() m=0��
m=0��
��1����mȡ��ֵʱ������һ��ʵ������
��2����mȡ��ֵʱ����������ʵ������
��3���跽�̵������ֱ�Ϊx1��x2����x1x2=m+1����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˽Ȿ�����꼶ѧ�������ڼ�μ����ʵ���������������˲������꼶ѧ�����ٲμ����ʵ�������������A������������5��������B������6��������C������7��������D������8��������E������9�켰���������������õ������ݻ��Ƴ�����������������ͳ��ͼ��
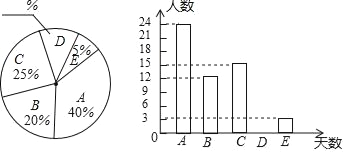
��������ϵ���Ϣ���ش��������⣺
��1����ȫ����ͳ��ͼ������ͳ��ͼ��
��2�������ѧ���μ����ʵ����������������� ����ѡ�A��B��C��D��E����
��3�����������꼶Լ��2000��ѧ����������Ʋμ����ʵ���������������7������ѧ����Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������
��1����ͼ�٣��ھ���ABCD�У�AB=2AD��EΪCD���е㣬���AEB�� ����ACB������������������=������
����̽��
��2����ͼ�ڣ���������ABCD�У�PΪCD���ϵ�һ�����㣬����Pλ�ںδ�ʱ����APB���˵�����ɣ�
������
��3����ͼ�ۣ���һ����¥AD��װ��һ����ι���ƣ�������ϡ��±������6�ף���AB=6�ף����±��ص�����ľ���BD=11.6�ף����С�յľ����������ĸ߶�EFΪ1.6�ף�����Զ�����Թ�����߽�ʱ����P�������Ч����ã��ӽ����������ͼ�����ҵ���P��λ�ã��������ʱС�����¥AD֮��ľ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
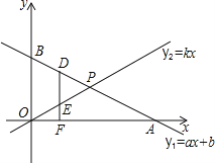
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y1=ax+b��ͼ����x�ᣬy�ύ��A��B����ֱ��y2=kx����P��2��1������PO=PA��
��1�����A�������k��ֵ��
��2����a��b��ֵ��
��3����DΪֱ��y1=ax+b��һ���㣬�������Ϊm����m��2����DF��x���ڵ�F����y2=kx�ڵ�E����DF=3EF�����D�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com