
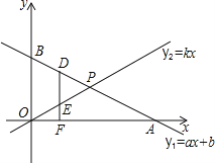
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b的图象与x轴,y轴交于A,B;与直线y2=kx交于P(2,1),且PO=PA.
(1)求点A的坐标和k的值;
(2)求a,b的值;
(3)点D为直线y1=ax+b上一动点,其横坐标为m,(m<2),DF⊥x轴于点F,交y2=kx于点E,且DF=3EF,求点D的坐标.
【答案】(1)点A坐标为![]() ,
,![]() ;(2)
;(2)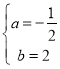 ;(3)点D坐标为
;(3)点D坐标为![]() 或
或![]() .
.
【解析】
(1)作![]() 于Q,利用等腰三角形的性质可求出点A坐标;根据点P坐标,利用待定系数法即可求出k的值;
于Q,利用等腰三角形的性质可求出点A坐标;根据点P坐标,利用待定系数法即可求出k的值;
(2)把![]() 两点坐标代入
两点坐标代入![]() ,解方程组即可解决问题;
,解方程组即可解决问题;
(3)先根据两个函数的解析式分别求出点D、E的纵坐标,再根据![]() ,构建方程即可解决问题.
,构建方程即可解决问题.
(1)如图,作![]() 于Q
于Q
![]()
![]()
∵![]()
∴![]() (等腰三角形的三线合一)
(等腰三角形的三线合一)
∴![]()
∴点A坐标为![]()
把![]() 代入
代入![]() 得
得![]()
解得![]() ;
;

(2)由题意,把![]() 代入
代入![]() 得
得![]()
解得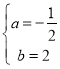 ;
;
(3)由(1)、(2)可知,![]()
∵点D横坐标为m,![]() 轴于点F
轴于点F
![]()
![]()
![]() 点D在点P左侧,即其纵坐标大于0
点D在点P左侧,即其纵坐标大于0
![]()
又![]()
![]()
分以下两种情况:
①当![]() 时,
时,![]()
解得![]() ,符合题设,此时
,符合题设,此时![]() ,则点D坐标为
,则点D坐标为![]()
②当![]() 时,
时,![]()
解得![]() ,符合题设,此时
,符合题设,此时![]() ,则点D坐标为
,则点D坐标为![]()
综上,所求的点D坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】平行四边形一边长为12cm,那么它的两条对角线的长度可以是( )
A. 8cm和14cm B. 10cm 和14cm C. 18cm和20cm D. 10cm和34cm
查看答案和解析>>
科目:初中数学 来源: 题型:
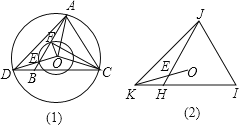
【题目】观察发现:如图(1),⊙O是△ADC的外接圆,点B是边CD上的一点,且△ABC是等边三角形.OD与AB交于点E,以O为圆心、OE为半径的圆交AB于点F,连接CF、OF.
(1)求∠AOD的度数;
(2)线段AE、CF有何大小关系?证明你的猜想.
拓展应用:如图(2),△HJI是等边三角形,点K是IH延长线上的一点.点O是△JKI的外接圆圆心,OK与JH相交于点E.如果等边三角形△JHI的边长为2,请直接写出JE的最小值和此时∠JEO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
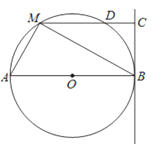
【题目】如图,直线BC与半径为6的⊙O相切于点B,点M是圆上的动点,过点M作MC⊥BC,垂足为C,MC与⊙O交于点D,AB为⊙O的直径,连接MA、MB,设MC的长为x,(6<x<12).
(1)当x=9时,求BM的长和△ABM的面积;
(2)是否存在点M,使MDDC=20?若存在,请求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
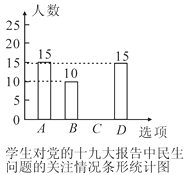
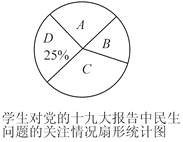
【题目】为学习贯彻党的十九大精神,我区各校积极开展了“党的十九大精神进校园”的宣讲活动,某校为了解学生对党的十九大报告中民生问题的关注情况,随机调查了部分学生,要求被调查的学生只能从A:生态环境、B:医疗卫生、C:文化教育、D:住房保障,四个方面中选择一项,根据调查结果,绘制了如下两幅不完整的统计图:
请解答下列问题:
(1)在扇形统计图中B所对应扇形的圆心角等于_____度,并补全条形统计图;
(2)甲乙两位同学对调查的四个方面都非常关注,他们从四个方面随机选择了一个,请用列表或画树状图的方法,求出他们恰好选择到同一个方面的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )

A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识链接:将两个含30°角的全等三角尺放在一起,让两个30°角合在一起成60°,经过拼凑、观察、思考,探究出“直角三角形中30°角所对的直角边等于斜边的一半”结论.
如图:等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF向右运动,已知点D、E都以每秒0.5cm的速度同时开始运动,运动过程中DE与BC相交于点P,设运动时间为x秒.
(1)请直接写出AD长.(用x的代数式表示)
(2)当△ADE为直角三角形时,运动时间为几秒?
(2)求证:在运动过程中,点P始终为线段DE的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
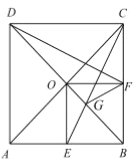
【题目】如图,在边长为1的正方形![]() 中,对角线
中,对角线![]() ,
,![]() 相交于点
相交于点![]() ,点
,点![]() ,点
,点![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,得到以下四个结论:①
,得到以下四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中正确的结论是________(填写序号).
,其中正确的结论是________(填写序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com