
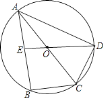
【题目】如图,⊙O是△ABC的外接圆,AC是直径,点E是AB的中点,延长EO交⊙O于D点,若BC=DC,AB=2 ![]() ,求
,求 ![]() 的长度.
的长度.
【答案】![]() .
.
【解析】
连结BD,如图,利用圆心角、弧、弦的关系,由BC=DC得![]() ,则根据垂径定理得到AC垂直平分BD,所以AB=AD,同样可得DA=DB,则可判断△ABD为等边三角形,所以∠BAC=30°,∠ABD=60°,根据圆周角定理得∠AOD=2∠ABD=120°,然后在Rt△AEO中计算出AO,最后利用弧长公式计算即可.
,则根据垂径定理得到AC垂直平分BD,所以AB=AD,同样可得DA=DB,则可判断△ABD为等边三角形,所以∠BAC=30°,∠ABD=60°,根据圆周角定理得∠AOD=2∠ABD=120°,然后在Rt△AEO中计算出AO,最后利用弧长公式计算即可.
连结BD,如图,
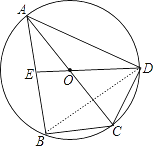
∵BC=DC,
∴![]() ,
,
∴AC垂直平分BD,
∴AB=AD,
∵点E是AB的中点,即AE=BE![]() ,
,
∴DE⊥AB,
∴DA=DB,
∴AB=AD=DB,
∴△ABD为等边三角形,
∴∠BAC=30°,∠ABD=60°,
∴∠AOD=2∠ABD=120°,
在Rt△AEO中,∵∠EAO=30°,
∴OE=![]() AE=1,AO=2OE=2,
AE=1,AO=2OE=2,
∴![]() 的长度=
的长度= ![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,且∠DAE=90°,连接CE.

(1)如图①,当点D在线段BC上时:
①BC与CE的位置关系为 ;
②BC、CD、CE之间的数量关系为 .
(2)如图②,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若不成立,请你写出正确结论,并给予证明.
(3)如图③,当点D在线段BC的延长线上时,BC、CD、CE之间的数量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
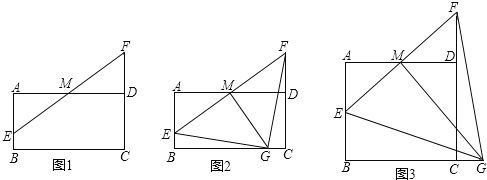
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连结EM并延长交线段CD的延长线于点F.
(1)如图1,求证:AE=DF;
(2)如图2,过点M作MG⊥EF交线段BC于点G,若ME=MG,求证:BE=CG;
(3)如图3,若AB=2![]() ,过点M作MG⊥EF交线段BC的延长线于点G.求线段AE长度的取值范围.
,过点M作MG⊥EF交线段BC的延长线于点G.求线段AE长度的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解本地七年级学生寒假期间参加社会实践活动情况,随机抽查了部分七年级学生寒假参加社会实践活动的天数(“A﹣﹣﹣不超过5天”、“B﹣﹣﹣6天”、“C﹣﹣﹣7天”、“D﹣﹣﹣8天”、“E﹣﹣﹣9天及以上”),并将得到的数据绘制成如下两幅不完整的统计图.
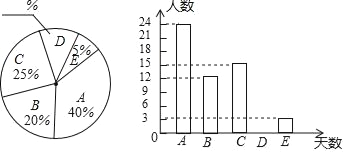
请根据以上的信息,回答下列问题:
(1)补全扇形统计图和条形统计图;
(2)所抽查学生参加社会实践活动天数的众数是 (选填:A、B、C、D、E);
(3)若该市七年级约有2000名学生,请你估计参加社会实践“活动天数不少于7天”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在矩形ABCD中,AB=2AD,E为CD的中点,则∠AEB ∠ACB(填“>”“<”“=”);
问题探究
(2)如图②,在正方形ABCD中,P为CD边上的一个动点,当点P位于何处时,∠APB最大?并说明理由;
问题解决
(3)如图③,在一幢大楼AD上装有一块矩形广告牌,其侧面上、下边沿相距6米(即AB=6米),下边沿到地面的距离BD=11.6米.如果小刚的睛睛距离地面的高度EF为1.6米,他从远处正对广告牌走近时,在P处看广告效果最好(视角最大),请你在图③中找到点P的位置,并计算此时小刚与大楼AD之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
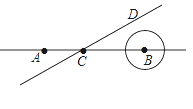
【题目】如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发多少秒直线CD恰好与⊙B相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
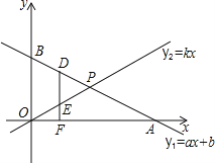
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b的图象与x轴,y轴交于A,B;与直线y2=kx交于P(2,1),且PO=PA.
(1)求点A的坐标和k的值;
(2)求a,b的值;
(3)点D为直线y1=ax+b上一动点,其横坐标为m,(m<2),DF⊥x轴于点F,交y2=kx于点E,且DF=3EF,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com