
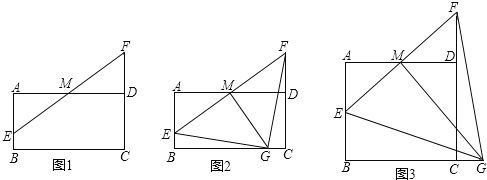
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连结EM并延长交线段CD的延长线于点F.
(1)如图1,求证:AE=DF;
(2)如图2,过点M作MG⊥EF交线段BC于点G,若ME=MG,求证:BE=CG;
(3)如图3,若AB=2![]() ,过点M作MG⊥EF交线段BC的延长线于点G.求线段AE长度的取值范围.
,过点M作MG⊥EF交线段BC的延长线于点G.求线段AE长度的取值范围.
【答案】(1)见解析;(2)见解析;(3)∴![]() <AE≤2
<AE≤2![]() .
.
【解析】
(1)根据矩形的性质得到∠EAM=∠FDM=90°,根据全等三角形的判定定理得到△AEM≌△DFM(ASA),由全等三角形的性质即可得到结论;
(2)如图2,由ME=MG可得△MEG是等腰直角△,再由ME=MF可得△EFG也是等腰直角△,即![]() ,
,![]() ;由
;由![]() 得
得![]() ,由
,由![]() 、
、![]() 、
、![]() ,得△BEG≌△CGF(AAS),得BE=CG;
,得△BEG≌△CGF(AAS),得BE=CG;
(3)根据四边形ABCD是矩形,得到∠A=∠ADC=90°,等量代换得到∠AEM=∠DMC,根据相似三角形的性质得到![]() ,代入数据求得AE=
,代入数据求得AE=![]() ,当E、B重合时,AE最长为2
,当E、B重合时,AE最长为2![]() ,于是得到结论.
,于是得到结论.
(1)如图1,
在矩形ABCD中,∠EAM=∠FDM=90°,
∵M是AD的中点,∴AM=DM,又∠AME=∠FMD,
在△AEM与△DFM中, 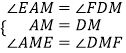 ,
,
∴△AEM≌△DFM(ASA),∴AE=DF;
(2)如图2,
∵ME=MG,MG⊥EF,
∴△MEG是等腰直角△;
同理,△EFG也是等腰直角△,
∴即![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 、
、![]() 、
、![]() ,
,
∴△BEG≌△CGF(AAS),
∴BE=CG;
(3)①当C、G重合时,如图4,

∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∴∠AME+∠AEM=90°,
∵MG⊥EF,
∴∠EMG=90°,
∴∠AME+∠DMC=90°,
∴∠AEM=∠DMC,
∴△AEM∽△DMC,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() ,
,
∴![]() <AE≤
<AE≤![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C,E为⊙O上的两点,AC平分∠EAB,CD⊥AE于D.
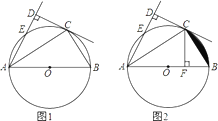
(1)求证:CD为⊙O的切线;
(2)过点C作CF⊥AB于F,如图2,判断CF和AF,DE之间的数量关系,并证明之;
(3)若AD-OA=1.5,AC=3![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形一边长为12cm,那么它的两条对角线的长度可以是( )
A. 8cm和14cm B. 10cm 和14cm C. 18cm和20cm D. 10cm和34cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(3,-2)在反比例函数y=![]() 的图象上,则下列点也在该反比例函数y=
的图象上,则下列点也在该反比例函数y=![]() 的图象的是( )
的图象的是( )
A. (3,-3) B. (1,6) C. (-2,3) D. (-2,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
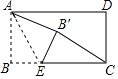
【题目】如图,点E是矩形纸片的边BC上的一动点,沿直线AE折叠纸片,点B落在了点B′位置,连结CB′.已知AB=3,BC=6,则当线段CB′最小时BE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
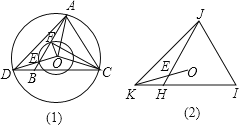
【题目】观察发现:如图(1),⊙O是△ADC的外接圆,点B是边CD上的一点,且△ABC是等边三角形.OD与AB交于点E,以O为圆心、OE为半径的圆交AB于点F,连接CF、OF.
(1)求∠AOD的度数;
(2)线段AE、CF有何大小关系?证明你的猜想.
拓展应用:如图(2),△HJI是等边三角形,点K是IH延长线上的一点.点O是△JKI的外接圆圆心,OK与JH相交于点E.如果等边三角形△JHI的边长为2,请直接写出JE的最小值和此时∠JEO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识链接:将两个含30°角的全等三角尺放在一起,让两个30°角合在一起成60°,经过拼凑、观察、思考,探究出“直角三角形中30°角所对的直角边等于斜边的一半”结论.
如图:等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF向右运动,已知点D、E都以每秒0.5cm的速度同时开始运动,运动过程中DE与BC相交于点P,设运动时间为x秒.
(1)请直接写出AD长.(用x的代数式表示)
(2)当△ADE为直角三角形时,运动时间为几秒?
(2)求证:在运动过程中,点P始终为线段DE的中点.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com