练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】定义：一个自然数，右边的数字总比左边的数字小，我们称它为“下滑数”（如：32，641，8531等）．现从两位数中任取一个，恰好是“下滑数”的概率为（　　）

    A. B. C. D.

    【答案】A

    【解析】分析：根据概率的求法，找准两点：①全部情况的总数：根据题意得知这样的两位数共有90个；
    ②符合条件的情况数目：从总数中找出符合条件的数共有45个；二者的比值就是其发生的概率．

    详解：两位数共有90个，下滑数有10、21、20、32、31、30、43、42、41、40、54、53、52、51、50、65、64、63、62、61、60、76、75、74、73、72、71、70、87、86、85、84、83、82、81、80、98、97、96、95、94、93、92、91、90共有45个，
    概率为．
    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，等腰△ABC的底边BC长为6，面积是36，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（　　）

    A.6B.10C.15D.16

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】雅安地震牵动着全国人民的心，某单位开展了“一方有难，八方支援”赈灾捐款活动.第一天收到捐款10 000元，第三天收到捐款12 100元.

    （1）如果第二天、第三天收到捐款的增长率相同，求捐款增长率；

    （2）按照（1）中收到捐款的增长速度，第四天该单位能收到多少捐款？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

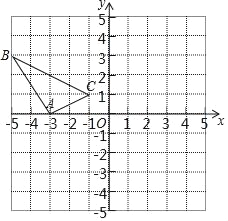
    【题目】在边长为1个单位长度的小正方形组成的网格中，建立如图所示的平面直角坐标系△ABC是格点三角形（顶点在网格线的交点上）

    （1）先作△ABC关于原点O成中心对称的△A1B1C1，再把△A1B1C1向上平移4个单位长度得到△A2B2C2；

    （2）△A2B2C2与△ABC是否关于某点成中心对称？若是，直接写出对称中心的坐标；若不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示是某公园为迎接“中国–南亚博览会”设置的一休闲区．，弧的半径长是米，是的中点，点在弧上，，则图中休闲区（阴影部分）的面积是（ ）

    A. 米 B. 米 C. 米 D. 米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】主题班会上，王老师出示了如图所示的一幅漫画，经过同学们的一番热议，达成以下四个观点：

    A．放下自我，彼此尊重； B．放下利益，彼此平衡；

    C．放下性格，彼此成就； D．合理竞争，合作双赢．

    要求每人选取其中一个观点写出自己的感悟．根据同学们的选择情况，小明绘制了下面两幅不完整的图表，请根据图表中提供的信息，解答下列问题：

    　观点

    频数　

    频率　

    　A

    　a

    　0.2

    　B

    　12

    　0.24

    　C

    　8

    　b

    　D

    　20

    　0.4

    （1）参加本次讨论的学生共有　 　人；表中a＝　 　，b＝　 　；

    （2）在扇形统计图中，求D所在扇形的圆心角的度数；

    （3）现准备从A，B，C，D四个观点中任选两个作为演讲主题，请用列表或画树状图的方法求选中观点D（合理竞争，合作双赢）的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中 过点A作AE⊥DC，垂足为E，连接BE，F为BE上一点，且∠AFE=∠D．

    （1）求证：△ABF∽△BEC；

    （2）若AD=5，AB=8，sinD=，求AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，和都是等边三角形，点在的延长线上．

    （1）找出图中一对全等三角形，并证明其全等；

    （2）求的度数？若，，求的长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（知识背景）

    我们在第十一章《三角形》中学习了三角形的边与角的性质，在第十二章《全等三角形》中学习了全等三角形的性质和判定，在十三章《轴对称》中学习了等腰三角形的性质和判定．在一些探究题中经常用以上知识转化角和边，进而解决问题．

    1.（问题初探）

    如图（1），△ABC中，∠BAC＝90°，AB＝AC，点D是BC上一点，连接AD，以AD为一边作△ADE，使∠DAE＝90°，AD＝AE，连接BE，猜想BE和CD有怎样的数量关系，并说明理由．

    2.（类比再探）

    如图（2），△ABC中，∠BAC＝90°，AB＝AC，点M是AB上一点，点D是BC上一点，连接MD，以MD为一边作△MDE，使∠DME＝90°，MD＝ME，连接BE，则∠EBD＝________．（直接写出答案，不写过程，但要求作出辅助线）

    3.（方法迁移）

    如图（3），△ABC是等边三角形，点D是BC上一点，连接AD，以AD为一边作等边三角形ADE，连接BE，则BE、BC之间有怎样的数量关系？________（直接写出答案，不写过程）．

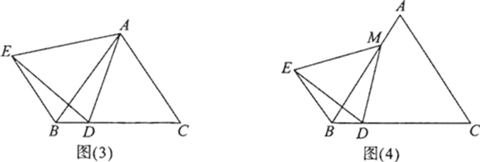
    4.（拓展创新）

    如图（4），△ABC是等边三角形，点M是AB上一点，点D是BC上一点，连接MD，以MD为一边作等边三角形MDE，连接BE．猜想∠EBD的度数，并说明理由．

    查看答案和解析>>

    同步练习册答案