Question

【题目】（知识背景）

我们在第十一章《三角形》中学习了三角形的边与角的性质，在第十二章《全等三角形》中学习了全等三角形的性质和判定，在十三章《轴对称》中学习了等腰三角形的性质和判定．在一些探究题中经常用以上知识转化角和边，进而解决问题．

1.（问题初探）

如图（1），△ABC中，∠BAC＝90°，AB＝AC，点D是BC上一点，连接AD，以AD为一边作△ADE，使∠DAE＝90°，AD＝AE，连接BE，猜想BE和CD有怎样的数量关系，并说明理由．

2.（类比再探）

如图（2），△ABC中，∠BAC＝90°，AB＝AC，点M是AB上一点，点D是BC上一点，连接MD，以MD为一边作△MDE，使∠DME＝90°，MD＝ME，连接BE，则∠EBD＝________．（直接写出答案，不写过程，但要求作出辅助线）

3.（方法迁移）

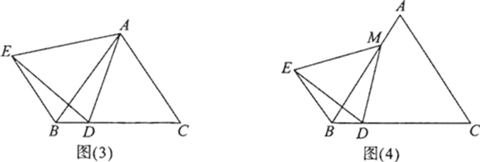
如图（3），△ABC是等边三角形，点D是BC上一点，连接AD，以AD为一边作等边三角形ADE，连接BE，则BE、BC之间有怎样的数量关系？________（直接写出答案，不写过程）．

4.（拓展创新）

如图（4），△ABC是等边三角形，点M是AB上一点，点D是BC上一点，连接MD，以MD为一边作等边三角形MDE，连接BE．猜想∠EBD的度数，并说明理由．

Answer 1

【答案】【问题初探】BE=CD，理由见解析；【类比再探】，如图所示，理由见解析；【方法迁移】BE=CD，理由见解析；【拓展创新】，理由见解析

【解析】

1.【问题初探】根据已知条件易证得，从而得到结论；

2.【类比再探】根据四点共圆的判定和性质，即可得到结论；

3.【方法迁移】根据已知条件易证得，从而得到结论；

4.【拓展创新】根据四点共圆的判定和性质，即可得到结论.

1.【问题初探】BE=CD，理由是：

∵∠EAD＝∠BAC=90，即：∠1+∠BAD＝∠2+∠BAD=90，

∴∠1＝∠2

又∵AD＝AE，AB＝AC，

∴，

∴BE=CD；

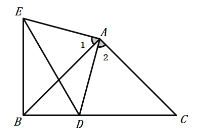
2.【类比再探】，如图所示：

∵与都是等腰直角三角形，

∴∠MED＝∠MBD=45，

∴B、D、M、E四点共圆，

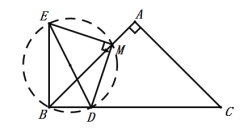
根据圆内接四边形对角互补，

∠EBD＝180-∠EMD，

故答案是：；

3.【方法迁移】BE=CD，理由是：

∵∠EAD＝∠BAC=60，即：∠1+∠BAD＝∠2+∠BAD=60，

∴∠1＝∠2

又∵AD＝AE，AB＝AC，

∴，

∴BE=CD；

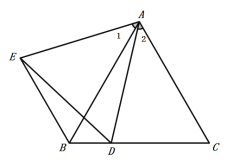
4.【拓展创新】，理由是：

∵与都是等边三角形，

∴∠MED＝∠MBD=60，

∴B、D、M、E四点共圆，如图所示：

根据圆内接四边形对角互补，

∠EBD＝180-∠EMD，

故答案是：