
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表


根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小李家装修,客厅共需某种型号的地砖100块,经市场调查发现,如果购买彩色地砖40块和单色地砖60块则共需花费5600元,如果购买彩色地砖和单色地砖各50块,则需花费6000元.
(1)求两种型号的地砖的单价各是多少元/块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且购买地砖的费用不超过3400元,那么彩色地砖最多能采购多少决?
查看答案和解析>>
科目:初中数学 来源: 题型:
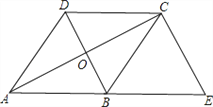
【题目】如图,已知菱形ABCD的对角线AC 、BD相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AC=![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
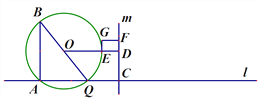
【题目】如图,点A在直线l上,点Q沿着直线l以3厘米/秒的速度由点A向右运动,以AQ为边作Rt![]() ,使∠BAQ=90°,
,使∠BAQ=90°,![]() ,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过
,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过![]() 的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=
的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=![]() CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.
CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.
(1)直接用含t的代数式表示BQ、DF;
(2)当0<t<1时,求矩形DEGF的最大面积;
(3)点Q在整个运动过程中,当矩形DEGF为正方形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年是改革开放四十周年,我国国内生产总值由改革开放前的3679亿元增至82.7万亿元数据82.7万亿用科学记数法表示为( )
A.8.27×105B.8.27×1013C.8.27×1012D.0.827×1014
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P,Q分别是双曲线![]() 在第一、三象限上的点,PA⊥
在第一、三象限上的点,PA⊥![]() 轴,QB⊥
轴,QB⊥![]() 轴,垂足分别为A,B,点C是PQ与
轴,垂足分别为A,B,点C是PQ与![]() 轴的交点.设△PAB的面积为
轴的交点.设△PAB的面积为![]() ,△QAB的面积为
,△QAB的面积为![]() ,△QAC的面积为
,△QAC的面积为![]() ,则有( )
,则有( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证: 
(1)AM⊥DM;
(2)M为BC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)下面的图形是由边长为l的正方形按照某种规律排列而组成的.
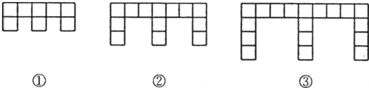
(1)观察图形,填写下表:
图形 | ① | ② | ③ |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com