
【题目】如图1,抛物线y1=ax2﹣![]() x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,
x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,![]() ),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.

(1)求抛物线y2的解析式;
(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;
(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)应用待定系数法求解析式;
(2)设出点T坐标,表示△TAC三边,进行分类讨论;
(3)设出点P坐标,表示Q、R坐标及PQ、QR,根据以P,Q,R为顶点的三角形与△AMG全等,分类讨论对应边相等的可能性即可.
(1)由已知,c=![]() ,
,
将B(1,0)代入,得:a﹣![]() =0,
=0,
解得a=﹣![]() ,
,
抛物线解析式为y1=![]() x2-
x2-![]() x+
x+![]() ,
,
∵抛物线y1平移后得到y2,且顶点为B(1,0),
∴y2=﹣![]() (x﹣1)2,
(x﹣1)2,
即y2=-![]() x2+
x2+![]() x-
x-![]() ;
;
(2)存在,
如图1:
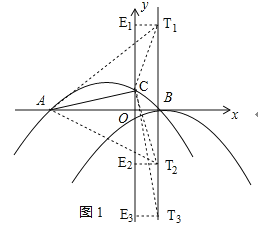
抛物线y2的对称轴l为x=1,设T(1,t),
已知A(﹣3,0),C(0,![]() ),
),
过点T作TE⊥y轴于E,则
TC2=TE2+CE2=12+(![]() )2=t2﹣
)2=t2﹣![]() t+
t+![]() ,
,
TA2=TB2+AB2=(1+3)2+t2=t2+16,
AC2=![]() ,
,
当TC=AC时,t2﹣![]() t+
t+![]() =
=![]() ,
,
解得:t1=![]() ,t2=
,t2=![]() ;
;
当TA=AC时,t2+16=![]() ,无解;
,无解;
当TA=TC时,t2﹣![]() t+
t+![]() =t2+16,
=t2+16,
解得t3=﹣![]() ;
;
当点T坐标分别为(1,![]() ),(1,
),(1,![]() ),(1,﹣
),(1,﹣![]() )时,△TAC为等腰三角形;
)时,△TAC为等腰三角形;
(3)如图2:
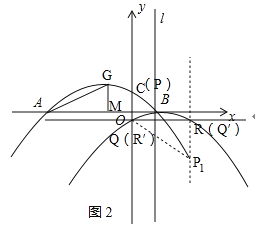
设P(m,![]() ),则Q(m,
),则Q(m,![]() ),
),
∵Q、R关于x=1对称
∴R(2﹣m,![]() ),
),
①当点P在直线l左侧时,
PQ=1﹣m,QR=2﹣2m,
∵△PQR与△AMG全等,
∴当PQ=GM且QR=AM时,m=0,
∴P(0,![]() ),即点P、C重合,
),即点P、C重合,
∴R(2,﹣![]() ),
),
由此求直线PR解析式为y=﹣![]() x+
x+![]() ,
,
当PQ=AM且QR=GM时,无解;
②当点P在直线l右侧时,
同理:PQ=m﹣1,QR=2m﹣2,
则P(2,﹣![]() ),R(0,﹣
),R(0,﹣![]() ),
),
PQ解析式为:y=﹣![]() ;
;
∴PR解析式为:y=﹣![]() x+
x+![]() 或y=﹣
或y=﹣![]() .
.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BF⊥AD,AD的延长线交BF于E,且E为垂足,则结论①AD=BF,②CF=CD,③AC+CD=AB,④BE=CF,⑤BF=2BE,其中正确的结论的个数是( )

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )

A. 6→3 B. 7→16 C. 7→8 D. 6→15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
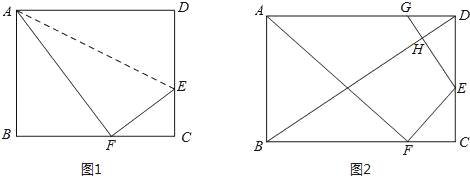
【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处.
(1)如图1,若折痕![]() ,且
,且![]() ,求矩形ABCD的周长;
,求矩形ABCD的周长;
(2)如图2,在AD边上截取DG=CF,连接GE,BD,相交于点H,求证:BD⊥GE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E是AD的中点,连接BE,BF平分∠EBC交CD于点F,交AC于点G,将△CGF沿直线GF折叠至△C′GF,BD与△C′GF相交于点M、N,连接CN,若AB=6,则四边形CNC′G的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
徐老师给爱好学习的小敏和小捷提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)…
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE. 可以证得:AE=DE(如图3)…
请你任意选择一种思路继续完成下一步的证明.
(变式探究)
“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变.(如图4),AB+BD=AC成立吗?若成立,请证明;若不成立,写出你的正确结论,并说明理由.
(迁移拓展)
△ABC中,∠B=2∠C. 求证:AC2=AB2+ABBC. (如图5)

查看答案和解析>>
科目:初中数学 来源: 题型:
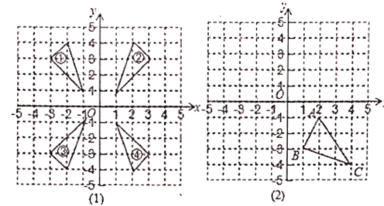
【题目】(1)在图(1)中编号①②③④的四个三角形中,关于y轴对称的两个三角形的编号为_________;关于x轴对称的两个三角形的编号为___________;
(2)在图(2)中,画出ΔABC关于x轴对称的图形ΔA1B1C1。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com