
����Ŀ���������龳��
����ʦ������ѧϰ��С����С���������һ�����⣺
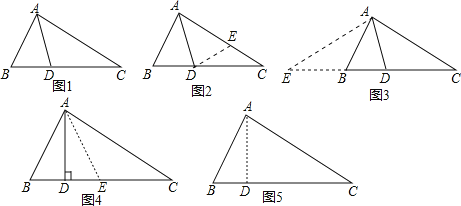
��ͼ1����ABC�У���B=2��C��AD����BAC��ƽ���ߣ���֤��AB+BD=AC
С����֤��˼·�ǣ���AC�Ͻ�ȡAE=AB������DE������ͼ2����
С�ݵ�֤��˼·�ǣ��ӳ�CB����E��ʹBE=AB������AE�� ����֤�ã�AE=DE����ͼ3����
��������ѡ��һ��˼·���������һ����֤����
����ʽ̽����
��AD����BAC��ƽ�������ij���AD��BC���ϵĸ����������������䣮����ͼ4����AB+BD=AC����������������֤��������������д�������ȷ���ۣ���˵�����ɣ�
��Ǩ����չ��
��ABC�У���B=2��C�� ��֤��AC2=AB2+ABBC�� ����ͼ5��

���𰸡�������
��������
���������龳��С����֤��˼·�ǣ���AC�Ͻ�ȡAE=AB���ɽ�ƽ���ߵ����ʾͿ��Եó���DAB=��DAE����֤����ADB��ADE�Ϳ��Եó����ۣ�С�ݵ�֤��˼·�ǣ��ӳ�CB����E��ʹBE=AB������AE���Ϳ��Եó���E=��C������AE=AC�������ó�AE=ED���ɣ�
��ʽ̽����CD�Ͻ�ȡDE=DB������AE����AD��BC�Ϳ��Եó�AE=AB����AED=��B������AED=��C+��CAE������C=��CAE�ó�AE=EC�������ó����ۣ�
Ǩ����չ������A��AD��BC��D���ɹ��ɶ����ã�AB2=BD2+AD2��AC2=CD2+AD2��AC2��AB2=CD2��BD2=BC��CD��BD�����ɣ�2���Ľ��۾Ϳ��Եó�AC2��AB2=BC��CD��BD��=BCAB���ɣ�
�⣺�����龳��С����֤��˼·�ǣ���ͼ2����AC�Ͻ�ȡAE=AB������DE������ͼ2��
��AD����BAC��ƽ���ߣ�
���BAD=��EAD��
����ABD����AED��
 ��
��
���ABD�ա�AED��SAS����
��BD=DE����ABD=��AED
�ߡ�AED=��EDC+��C����B=2��C��
���EDC=��C��
��DE=EC��
��AB+BD=AC��
С�ݵ�֤��˼·�ǣ���ͼ3���ӳ�CB����E��ʹBE=AB������AE��
���E=��BAE��
�ߡ�ABC=��E+��BAE��
���ABC=2��E��
�ߡ�ABC=2��C��
���E=��C��
���AEC�ǵ��������Σ�
��AD����BAC��ƽ���ߣ�
���BAD=��DAC��
�ߡ�ADE=��DAC+��C����DAE=��BAD+��BAE
���ADE=��DAE��
��EA=ED=AC��
��AB+BD=AC��
��ʽ̽����
AB+BD=AC������ ��ȷ���ۣ�AB+BD=CD����5�֣�
���ɣ���ͼ4����CD�Ͻ�ȡDE=DB������AE��
��AD��BC��
��AD��BE���д��ߣ�
��AE=AB��
���B=��AED��
�ߡ�AED=��C+��CAE������B=2��C��
���C=��CAE��
��AE=EC��
��AB+BD=CD��
Ǩ����չ��
֤������ͼ5������A��AD��BC��D���ɹ��ɶ����ã�AB2=BD2+AD2��AC2=CD2+AD2��
��AC2��AB2=CD2��BD2=��CD+BD����CD��BD��=BC��CD��BD��
��AB+BD=CD��
��CD��BD=AB��
��AC2��AB2=BC��CD��BD��=BCAB��
��AC2=AB2+ABBC��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳���4����E��AB����һ���㣬����CE������B��BG��CE�ڵ�G����P��AB������һ���㣬��PD+PG����СֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����A��B�������г���A�����г��ۼ�Ϊ2 100Ԫ/����B�����г��ۼ�Ϊ1 750Ԫ/����ÿ��A�����г��Ľ��۱�ÿ��B�����г��Ľ��۶�400Ԫ���̳���80 000Ԫ����A�����г�����������64 000Ԫ����B�����г���������ȣ�
��1����ÿ��A��B�������г��Ľ��۷ֱ��Ƕ��٣�
��2�������̳���һ�ι������������г���100�����蹺��A�����г�m������100�����г�������������ΪyԪ��Ҫ��B�����г�����������A�����г�������2������������13 000Ԫ����������ķ����Լ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y1=ax2��![]() x+c��x�ύ�ڵ�A�͵�B��1��0������y�ύ�ڵ�C��0��
x+c��x�ύ�ڵ�A�͵�B��1��0������y�ύ�ڵ�C��0��![]() ����������y1�Ķ���ΪG��GM��x���ڵ�M����������y1ƽ�ƺ�õ�����ΪB�ҶԳ���Ϊֱ��l��������y2��
����������y1�Ķ���ΪG��GM��x���ڵ�M����������y1ƽ�ƺ�õ�����ΪB�ҶԳ���Ϊֱ��l��������y2��

��1����������y2�Ľ���ʽ��
��2����ͼ2����ֱ��l���Ƿ���ڵ�T��ʹ��TAC�ǵ��������Σ������ڣ���������е�T�����ꣻ�������ڣ���˵�����ɣ�
��3����PΪ������y1��һ���㣬����P��y���ƽ���߽�������y2�ڵ�Q����Q����ֱ��l�ĶԳƵ�ΪR������P��Q��RΪ���������������AMGȫ�ȣ���ֱ��PR�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����10��10�����������У�ÿ��С�����εı߳���Ϊ1����λ������ABC����ƽ��4����λ���õ���A��B��C�����ٰ���A��B��C���Ƶ�C'˳ʱ����ת90�����õ���A��B��C�䣬
��1�����㻭����A��B��C������A��B��C������Ҫ��д��������
��2������߶�A��C������ת��������ɨ��������������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣬��ABC��30�㣬��CDE�ǵȱ������Σ���D�ڱ�AB�ϣ�

��1����ͼ1������E�ڱ�BC��ʱ����֤DE��EB��
��2����ͼ2������E�ڡ�ABC�ڲ�ʱ������ED��EB������ϵ��������֤����
��3����ͼ3������E�ڡ�ABC�ⲿʱ��EH��AB�ڵ�H������E��GE��AB�����߶�AC���ӳ����ڵ�G��AG��5CG��BH��3����CG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���ֱ��������ABC�У���ABC=90����DΪAC���ϵ��е㣬��D����DE��DF����AB�ڵ�E����BC�ڵ�F����AE=8��FC=6.
��1����EF�ij�.
��2�����ı���BEDF�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=6��BC=8��AD����BAC��ƽ���ߣ���P��Q�ֱ���AD��AC�ϵĶ��㣬��PC+PQ����Сֵ�ǣ� ��

A. ![]() B. 4 C.
B. 4 C. ![]() D. 5
D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������5000Ԫ����ij�ָɹ����ۣ���������״�����ã������ֵ���9000Ԫ�ʽ����ָɹ��������ÿǧ�˵Ľ��۱ȵ�һ�εĽ��������5Ԫ�������ɹ������ǵ�һ�ε�1.5����
��1�����ָɹ��ĵ�һ�ν�����ÿǧ�˶���Ԫ��
��2��������а�ÿǧ��40Ԫ�ļ۸���ۣ����ָɹ��۳������µ�100ǧ�˰��ۼ۵�6�����꣬�����������ָɹ���ӯ������Ԫ��
��3������������ɹ�ÿǧ���ۼ���ͬ����ȫ������������Բ�����25%����ôÿǧ�˸ɹ����ۼ������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com