练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

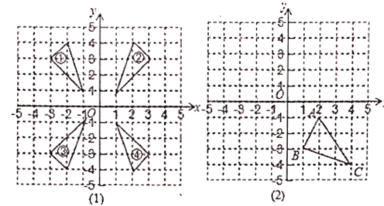
    【题目】（1）在图(1)中编号①②③④的四个三角形中，关于y轴对称的两个三角形的编号为_________；关于x轴对称的两个三角形的编号为___________；

    （2）在图(2)中，画出ΔABC关于x轴对称的图形ΔA1B1C1。

    【答案】(1)①②、③④；①③、②④；(2)见解析

    【解析】

    （1）根据轴对称图形的性质得出关于x轴或y轴对称的图形.

    （2）再根据关于x轴对称的图形的特点画出△ABC关于x轴对称的图形△A1B1C1．

    （1）∵①与②，③与④图形中各对应点关于y轴对称，
    ∴①与②或③与④关于y轴对称；
    ∵①与③，②与④图形中各对应点关于x轴对称，
    ∴①与③或②与④关于x轴对称．
    故答案为：①②或③④，①③或②④．
    （2）如图，由图可知，A1（2，1），B1（1，3），C1（4，4）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下列解题过程：

    ===-2；

    ==．

    请回答下列问题：

    （1）观察上面的解题过程，请直接写出式子=　 　；

    （2）观察上面的解题过程，请直接写出式子=　 　；

    （3）利用上面所提供的解法，请求+···+的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线y1=ax2﹣x+c与x轴交于点A和点B（1，0），与y轴交于点C（0，），抛物线y1的顶点为G，GM⊥x轴于点M．将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2．

    （1）求抛物线y2的解析式；

    （2）如图2，在直线l上是否存在点T，使△TAC是等腰三角形？若存在，请求出所有点T的坐标；若不存在，请说明理由；

    （3）点P为抛物线y1上一动点，过点P作y轴的平行线交抛物线y2于点Q，点Q关于直线l的对称点为R，若以P，Q，R为顶点的三角形与△AMG全等，求直线PR的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB＝90°，∠ABC＝30°，△CDE是等边三角形，点D在边AB上．

    （1）如图1，当点E在边BC上时，求证DE＝EB；

    （2）如图2，当点E在△ABC内部时，猜想ED和EB数量关系，并加以证明；

    （3）如图3，当点E在△ABC外部时，EH⊥AB于点H，过点E作GE∥AB，交线段AC的延长线于点G，AG＝5CG，BH＝3．求CG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰直角三角形ABC中，∠ABC=90°，D为AC边上的中点，过D点作DE⊥DF，交AB于点E，交BC于点F，若AE=8，FC=6.

    （1）求EF的长.

    （2）求四边形BEDF的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC 中，AB=AC，CD是∠ACB的平分线，DE∥BC，交AC于点 E．

    （1）求证：DE=CE．

    （2）若∠CDE=35°，求∠A 的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是（ ）

    A. B. 4 C. D. 5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知和都是等腰直角三角形，点D是直线BC上的一动点（点D不与B、C重合），连接CE．

    （1）在图1中，当点D在边BC上时，求证：；

    （2）在图2中，当点D在边BC的延长线上时，结论是否还成立？若不成立，请猜想BC、CE、CD之间存在的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AO平分∠BAC，AO⊥BC，DE⊥BC，GH⊥BC，垂足分别为O、E、H，且DO∥AC，∠B=43°，则图中角的度数为47°的角的个数是（　　）

    A. 5 B. 6 C. 7 D. 8

    查看答案和解析>>

    同步练习册答案