
【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A 的度数.

【答案】(1)见解析;(2) 40°.
【解析】
(1)根据角平分线的性质可得出∠BCD=∠ECD,由DE∥BC可得出∠EDC=∠BCD,进而可得出∠EDC=∠ECD,再利用等角对等边即可证出DE=CE;
(2)由(1)可得出∠ECD=∠EDC=35°,进而可得出∠ACB=2∠ECD=70°,再根据等腰三角形的性质结合三角形内角和定理即可求出∠A的度数.
(1)∵CD是∠ACB的平分线,∴∠BCD=∠ECD.
∵DE∥BC,∴∠EDC=∠BCD,∴∠EDC=∠ECD,∴DE=CE.
(2)∵∠ECD=∠EDC=35°,∴∠ACB=2∠ECD=70°.
∵AB=AC,∴∠ABC=∠ACB=70°,∴∠A=180°﹣70°﹣70°=40°.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=CB,点E在边BC上,点F在边AB的延长线上,BE=BF.
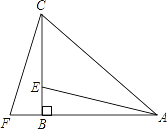
(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】纸箱厂用如图1所示的长方形和正方形纸板,做成如图2所示的竖式与横式两种长方体形状的有底无盖纸盒.

(1)现有正方形纸板172张,长方形纸板330张.若要做两种纸盒共l00个,设做竖式纸盒x个.
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) |
x | ||
正方形纸板(张) | 2(100-x) | |
长方形纸板(张) | 4x |
②按两种纸盒的数量分,有哪几种生产方案?
(2)若有正方形纸板112张,长方形纸板![]() 张,做成上述两种纸盒,纸板恰好用完.已知100<
张,做成上述两种纸盒,纸板恰好用完.已知100<![]() <110,则
<110,则![]() 的值是 .
的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,则BD的长为( )

A. 5cm B. 6cm C. 7cm D. 8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c与x轴交于点A(1,0),B(3,0),与y轴交于点C. 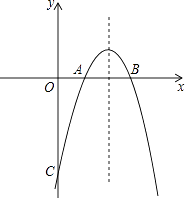
(1)求抛物线的解析式;
(2)设点P在该抛物线上滑动,则满足S△PAB=1的点P有几个?求出所有点P的坐标;
(3)在该抛物线的对称轴上存在点M,使得△MAC的周长最小,求出这个点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°. 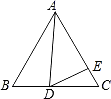
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB中,OA=OB=10,∠AOB=70°,以点O为圆心,6为半径的优弧 ![]() 分别交OA、OB于点M,N.
分别交OA、OB于点M,N. 
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转70°得OP′.求证:AP=BP′;
(2)点T在左半弧上,若AT与弧相切,求点T到OA的距离;
(3)设点Q在优弧 ![]() 上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com