
【题目】如图,在△ABC中,∠ABC=90°,AB=CB,点E在边BC上,点F在边AB的延长线上,BE=BF.
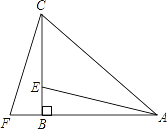
(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
【答案】(1)见解析;(2)∠ACF的度数为60°
【解析】
(1)由∠ABC=90°可得∠CBF=90°,再由SAS就即可得出△ABE≌△CBF;
(2)根据题意可得∠BAC=∠ACB=45°由∠CAE=30°可得∠BAE=15°,即∠BCF=15°,进而可以求出∠ACF的度数.
(1)证明:∵∠ABC=90°,
∴∠ABC=∠CBF=90°.
在△ABE和△CBF中,
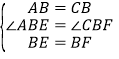 ,
,
∴△ABE≌△CBF(SAS);
(2)解:∵△ABE≌△CBF,
∴∠BAE=∠BCF,
∵∠ABC=90°,AB=CB,
∴∠BCA=∠BAC=45°,
∵∠CAE=30°,
∴∠BAE=15°,
∴∠BCF=15°,
∵∠ACF=∠BCF+∠ACB,
∴∠ACF=15°+45°=60°.
答:∠ACF的度数为60°.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E分别为AB、AC上的点,∠BDE、∠CED的平分线分别交BC于点F、G,EG∥AB.若∠BGE=110°,则∠BDF的度数为___________
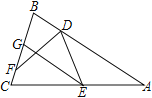
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是 ( )

A. ![]() B.
B. ![]() C. 6 D. 3
C. 6 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于下列各组条件,不能判定△![]() ≌△
≌△![]() 的一组是 ( )
的一组是 ( )
A. ∠A=∠A′,∠B=∠B′,AB=A′B′
B. ∠A=∠A′,AB=A′B′,AC=A′C′
C. ∠A=∠A′,AB=A′B′,BC=B′C′
D. AB=A′B′,AC=A′C′,BC=B′C′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,P为等边△ABC内一点,∠APB=113°,∠APC=123°,试说明:以AP,BP,CP为边长可以构成一个三角形,并确定所构成三角形的各内角的度数. 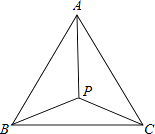
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A 的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com