
【题目】在Rt△ABC中,∠ACB=90°,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,则BD的长为( )

A. 5cm B. 6cm C. 7cm D. 8cm
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】对于下列各组条件,不能判定△![]() ≌△
≌△![]() 的一组是 ( )
的一组是 ( )
A. ∠A=∠A′,∠B=∠B′,AB=A′B′
B. ∠A=∠A′,AB=A′B′,AC=A′C′
C. ∠A=∠A′,AB=A′B′,BC=B′C′
D. AB=A′B′,AC=A′C′,BC=B′C′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣8mx+16m﹣1(m>0)与x轴的交点分别为A(x1 , 0),B(x2 , 0).
(1)求证:抛物线总与x轴有两个不同的交点;
(2)若AB=2,求此抛物线的解析式.
(3)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2﹣8mx+16m﹣1(m>0)与线段CD有交点,请写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
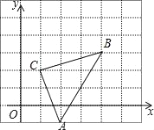
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2)
(1)写出点A、B的坐标:A( , )、B( , )
(2)将△ABC先向左平移1个单位长度,再向上平移2个单位长度,得到△A′B′C′,画出△A′B′C′
(3)写出三个顶点坐标A′( 、 )、B′( 、 )、C′ ( 、 )
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(2,3),B(1,1),C(4,1),M(6,3).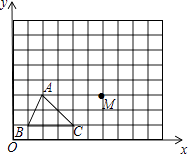
(1)将△ABC平原得到△A1B1C1 , 其中点A,B,C的对应点分别是A1 , B1 , C1 , 且点A1的坐标是(3,6),在图中画出△A1B1C1 .
(2)将(1)中的△A1B1C1绕点M顺时针旋转90°,画出旋转后的△A2B2C2(其中点A2 , B2 , C2的对应点分别是A1 , B1 , C1),并写出点A2 , B2 , C2的坐标.
(3)(2)中的△A2B2C2能通过旋转△ABC得到吗?若能,请写出旋转的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过点B(1,4),且与直线y=﹣x﹣11平行.
(1)求直线AB的解析式并求出点C的坐标;
(2)根据图象,写出关于x的不等式0<2x﹣4<kx+b的解集;
(3)现有一点P在直线AB上,过点P作PQ∥y轴交直线y=2x﹣4于点Q,若线段PQ的长为3,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,铅球运行路线如图.
,铅球运行路线如图. 
(1)求铅球推出的水平距离;
(2)通过计算说明铅球行进高度能否达到4m?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com