
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
【答案】
(1)证明:∵△=(2k+1)2﹣4(k2+k)=1>0,
∴方程有两个不相等的实数根
(2)解:一元二次方程x2﹣(2k+1)x+k2+k=0的解为x= ![]() ,即x1=k,x2=k+1,
,即x1=k,x2=k+1,
∵k<k+1,
∴AB≠AC.
当AB=k,AC=k+1,且AB=BC时,△ABC是等腰三角形,则k=5;
当AB=k,AC=k+1,且AC=BC时,△ABC是等腰三角形,则k+1=5,解得k=4,
综合上述,k的值为5或4
【解析】(1)先计算出△=1,然后根据判别式的意义即可得到结论;(2)先利用公式法求出方程的解为x1=k,x2=k+1,然后分类讨论:AB=k,AC=k+1,当AB=BC或AC=BC时△ABC为等腰三角形,然后求出k的值.


科目:初中数学 来源: 题型:
【题目】如图,已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图①,求证:OB∥AC. 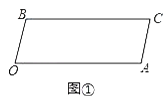
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度数. 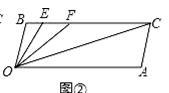
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值. 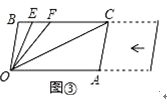
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A、B表示的数分别是有理数a,b.
(1)若点A在原点的左侧,点B在原点的右侧,且|a|=|b|,则a与b的关系是 ,用式子表示为 .
(2)若a=﹣5,b=1![]()
①分别写出a,b的相反数;
②求|a![]() |﹣|b
|﹣|b![]() |的值.
|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国庆节大酬宾”,某商场设计的促销活动如下:在一个不透明的箱子里放有3个质地相同的小球,并在球上分别标有“5元”、“10元”和“15元”的字样,规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两个小球所标金额和返还相等价格的购物券,购物券可以在本商场消费,某顾客刚好消费300元.
(1)该顾客最多可得到元购物券;
(2)请你用画树状图和列表的方法,求出该顾客所得购物券的金额不低于25元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中标明了小英家附近的一些地方,已知游乐场的坐标为(3,2).
(1)在图中建立平面直角坐标系,并写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2),(3,-1),(1,-1),(-1,-2),(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格(边长为1的小正方形组成的网格纸,正方形的顶点称为格点)是我们在初中阶段常用的工具,利用它可以解决很多问题.
(1)如图①中,△ABC是格点三角形(三个顶点为格点),则它的面积为 ;
(2)如图②,在4×4网格中作出以A为顶点,且面积最大的格点正方形(四个顶点均为格点);
(3)人们发现,记格点多边形(顶点均为格点)内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为S=ma+nb-1,其中m,n为常数.试确定m,n的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com