
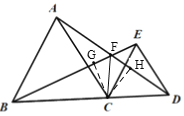
【题目】已知,如图△ABC和△CDE均为等边三角形,B、C、D三点在同一条直线上,连接线段BE、AD交于点F,连接CF,

(1)求证:∠FBC=∠FAC.
(2)求∠BFC的度数.
【答案】(1)证明见解析;(2)∠BFC=60°.
【解析】
(1)根据等边三角形的性质可得∠ECD=∠ABC=60°,AC=BC,CD=CE,利用角的和差关系可得∠ACD=∠BCE,利用SAS可证明△ACD≌△BCE,根据全等三角形的性质即可得答案;(2)作CG⊥BE于G,CH⊥AD于H,由∠ACB=∠EDC=60°可得AC//ED,根据平行线的性质可得∠CAD=∠ADE,利用等量代换可得∠EBD=∠ADE,根据三角形外角性质可得∠EFD=∠EBD+∠BDF=∠ADE+∠BDF=∠BDE=60°,根据平角的定义可得∠BFD=120°,由(1)得△ACD≌△BCE,根据全等三角形对应边上的高对应相等可得CG=CH,根据角平分线的性质可得CF是∠BFD的角平分线,即可求出∠BFC的度数.
(1)∵△ABC和△CDE均为等边三角形,
∴AC=BC,∠ACB=∠ECD=60°,CD=CE,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠ACD=∠BCE,
在△ACD和△BCE中, ,
,
∴△ACD≌△BCE,
∴∠EBC=∠DAC,即∠FBC=∠FAC.
(2)∵∠ACB=∠EDC=60°,
∴AC//DE,
∴∠CAD=∠ADE,
∵∠CAD=∠EBD,
∴∠EBD=∠ADE,
∴∠EFD=∠EBD+∠BDF=∠ADE+∠BDF=∠EDB=60°,
∴∠BFD=180°-∠EFD=120°,
∵△ACD≌△BCE,CG、CH分别是对应边BE、AD的高,
∴CG=CH,
∴CF是∠BFD的角平分线,
∴∠BFC=![]() ∠BFD=60°.
∠BFD=60°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(知识背景)
我们在第十一章《三角形》中学习了三角形的边与角的性质,在第十二章《全等三角形》中学习了全等三角形的性质和判定,在十三章《轴对称》中学习了等腰三角形的性质和判定.在一些探究题中经常用以上知识转化角和边,进而解决问题.
1.(问题初探)
如图(1),△ABC中,∠BAC=90°,AB=AC,点D是BC上一点,连接AD,以AD为一边作△ADE,使∠DAE=90°,AD=AE,连接BE,猜想BE和CD有怎样的数量关系,并说明理由.

2.(类比再探)
如图(2),△ABC中,∠BAC=90°,AB=AC,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作△MDE,使∠DME=90°,MD=ME,连接BE,则∠EBD=________.(直接写出答案,不写过程,但要求作出辅助线)
3.(方法迁移)
如图(3),△ABC是等边三角形,点D是BC上一点,连接AD,以AD为一边作等边三角形ADE,连接BE,则BE、BC之间有怎样的数量关系?________(直接写出答案,不写过程).
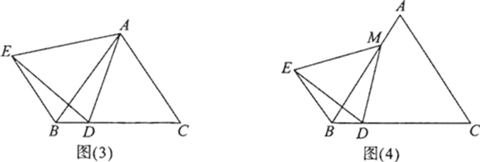
4.(拓展创新)
如图(4),△ABC是等边三角形,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作等边三角形MDE,连接BE.猜想∠EBD的度数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为18,BP=4,则AB的长为_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ ABC中,∠ ABC=90°,AB=BC,D在边 AC上,AE┴ BD于 E.
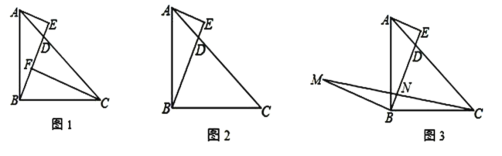
(1) 如图 1,作 CF⊥ BD于 F,求证:CF-AE=EF;
(2) 如图 2,若 BC=CD,求证:BD=2AE ;
(3) 如图3,作 BM ⊥BE,且 BM=BE,AE=2,EN=4,连接 CM交 BE于 N,请直接写出△BCM的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<![]() <3,∴
<3,∴![]() 的整数部分为2,小数部分为
的整数部分为2,小数部分为![]() ﹣2.
﹣2.
请解答:
(1)![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a, ![]() 的整数部分为b,求a+b-
的整数部分为b,求a+b-![]() 的值;
的值;
(3)已知:x是3+![]() 的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)画出△ABC关于y轴对称的图形△A′B′C′,并写出点A′、B'、C′的坐标;
(2)在图中找一点D,以D、B、C为顶点画三角形,使它与△ABC全等,请画出所有符合条件的△DBC(点D与点A重合除外),并直接写出点D的坐标.(提示:当点D不唯一时,可用D1、D2、D3等加以区别)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com