
【题目】如图,在△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为18,BP=4,则AB的长为_____________

【答案】7
【解析】
根据角平分线的定义得到∠CBQ=![]() ∠ABC,再由等角对等边得到CQ=BQ,得到BQ+AQ=CQ+AQ=AC;过点P作PD∥BQ,由“AAS”可证△ABP≌△ADP,由全等三角形的性质可得AB=AD,BP=DP,得到AB+BP=AD+CD=AC,即BQ+AQ=AB+BP,即可得出AB的长.
∠ABC,再由等角对等边得到CQ=BQ,得到BQ+AQ=CQ+AQ=AC;过点P作PD∥BQ,由“AAS”可证△ABP≌△ADP,由全等三角形的性质可得AB=AD,BP=DP,得到AB+BP=AD+CD=AC,即BQ+AQ=AB+BP,即可得出AB的长.
解:∵BQ是∠ABC的角平分线,
∴∠CBQ=![]() ∠ABC.
∠ABC.
又∵∠ABC=2∠C,
∴∠CBQ=![]() ∠ABC=∠C,
∠ABC=∠C,
∴ BQ=CQ,
∴ BQ+AQ=CQ+AQ=AC(1).
如图所示,过点P作PD∥BQ交CQ于点D,
则∠CPD=∠CBQ,∠ADP=∠AQB,
∵∠AQB=∠C+∠CBQ=2∠C,
∴∠ADP=2∠C,
∴∠ABC=∠ADP.
又∵AP是∠BAC的角平分线,
∴∠BAP=∠CAP.
在△ABP和△ADP中,
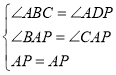 ,
,
∴△ABP≌△ADP(AAS),
∴AB=AD,BP=DP,
∴AB+BP=AD+CD=AC(2),
由(1)(2)得:BQ+AQ=AB+BP,
又∵△ABQ的周长为18,BP=4,
∴18-AB= AB+4,
∴ AB=7.
故答案为:7.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,B、A、F三点在同一直线上,(1)AD∥BC,(2)∠B=∠C,(3)AD平分∠EAC.
请你用其中两个作为条件,另一个作为结论,构造一个真命题,并证明.
己知:______________________________________________________.
求证:______________________________________________________.
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
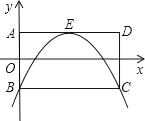
【题目】在矩形ABCD中,AB=2,AD=4,以AB的垂直平分线为x轴,AB所在的直线为y轴,建立如图所示的平面直角坐标系.
(1)求点的坐标:A ,B ,C , ,AD的中点E ;
(2)求以E为顶点,对称轴平行于y轴,并且经过点B,C的抛物线的解析式;
(3)求对角线BD与上述抛物线除点B以外的另一交点P的坐标;
(4)△PEB的面积S△PEB与△PBC的面积S△PBC具有怎样的关系?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4,

(1)在如图所示的平面直角坐标系中,画出函数的图象.
(2)求图象与x轴的交点A的坐标,与y轴交点B的坐标.
(3)利用图象直接写出:当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图△ABC和△CDE均为等边三角形,B、C、D三点在同一条直线上,连接线段BE、AD交于点F,连接CF,

(1)求证:∠FBC=∠FAC.
(2)求∠BFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
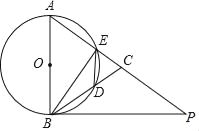
【题目】在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,P为AC延长线上一点,且∠PBC=![]() ∠BAC,连接DE,BE.
∠BAC,连接DE,BE.
(1)求证:BP是⊙O的切线;
(2)若sin∠PBC=![]() ,AB=10,求BP的长.
,AB=10,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达
两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达![]() 地后马上以另一速度原路返回
地后马上以另一速度原路返回![]() 地(掉头的时间忽略不计),乙车到达
地(掉头的时间忽略不计),乙车到达![]() 地以后即停在
地以后即停在![]() 地等待甲车.如图所示为甲乙两车间的距离
地等待甲车.如图所示为甲乙两车间的距离![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (小时)之间的函数图象,则当乙车到达
(小时)之间的函数图象,则当乙车到达![]() 地的时候,甲车与
地的时候,甲车与![]() 地的距离为__________千米.
地的距离为__________千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com