
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

【答案】(1)C(1,-4).(2)证明见解析;(3)∠APB=135°,P(1,0).
【解析】试题分析:(1)过C作CD⊥Y轴于D,证出△ABO≌△BCD,再由OB=DC,OA=DB得出C(1,-4);
(2)证出△APB≌△CQB,进而得出PA=CQ;
(3)由C、P、Q三点共线,得∠CQB=135°,即∠APB=135°,进而∠OPB=45°,得P(1,0).
试题解析:(1)过C作CD⊥Y轴于D,
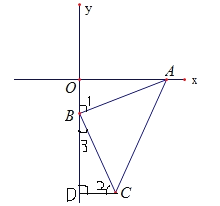
∴∠AOB=∠BDC=90°, ∠2+∠3=90°,
∵BC⊥AB,
∴∠1+∠3=90°,
∴∠1=∠2,
在△ABO和△BCD中, 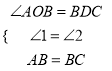 ,
,
∴△ABO≌△BCD,
∴OB=DC, OA=DB
∴C(1,-4);
(2)∵∠ABQ+∠QBC=∠PBA+∠ABQ=90°,
∴∠QBC=∠PBA,
在△APB和△CQB中, 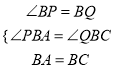 ,
,
∴△APB≌△CQB,(AAS)
∴AP=CQ;
(2)∵△APB≌△CQB,
∴∠APB=∠CQB,
∵由C、P、Q三点共线,
∴∠CQB=135°,即∠APB=135°,
∴∠OPB=45°,
∴P(1,0).


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() (x>0)的图象相交于A(2,3),B(a,1)两点.
(x>0)的图象相交于A(2,3),B(a,1)两点.
(1)求这两个函数表达式;
(2)求证:AB=2BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地管辖A,B,C,D四个镇,其中C,A,D三个镇在一条直线上,相互两镇之间的公路里程如图所示,由于大山阻隔,原来从A,C两镇去D镇都需绕到B镇前往.为了发展经济,缩短A,C两镇到D镇的路程,现决定开凿隧道修通A,C两镇直达D镇的公路AD.公路修通后从A镇去D镇的路程比原来缩短了多少千米?(参考数据:![]() =32,
=32,![]() ≈46.65)
≈46.65)
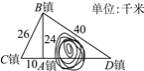
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学就餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.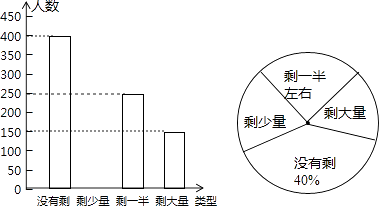
(1)这次被调查的同学共有名;
(2)补全条形统计图;
(3)计算在扇形统计图中剩大量饭菜所对应扇形圆心角的度数;
(4)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校20000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1 , 旋转角为θ(0°<θ<90°),连接AC1、BD1 , AC1与BD1交于点P.
(1)如图1,若四边形ABCD是正方形.请直接写出AC1 与BD1的数量关系和位置关系.
(2)如图2,若四边形ABCD是菱形,AC=6,BD=8,判断AC1与BD1的数量关系和位置关系,并给出证明;
(3)如图3,若四边形ABCD是平行四边形,AC=6,BD=12,连接DD1 , 设AC1=kBD1 , 请直接写出k的值和AC12+(kDD1)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP.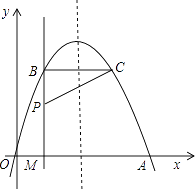
(1)当m=3时,求点A的坐标及BC的长;
(2)当m>1时,连接CA,问m为何值时CA⊥CP?
(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于分式的判断,正确的是( )
A.当x=2时, ![]() 的值为零
的值为零
B.无论x为何值, ![]() 的值总为正数
的值总为正数
C.无论x为何值, ![]() 不可能得整数值
不可能得整数值
D.当x≠3时, ![]() 有意义
有意义
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C,其中正确的结论有______.
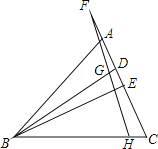
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com