
【题目】某地管辖A,B,C,D四个镇,其中C,A,D三个镇在一条直线上,相互两镇之间的公路里程如图所示,由于大山阻隔,原来从A,C两镇去D镇都需绕到B镇前往.为了发展经济,缩短A,C两镇到D镇的路程,现决定开凿隧道修通A,C两镇直达D镇的公路AD.公路修通后从A镇去D镇的路程比原来缩短了多少千米?(参考数据:![]() =32,
=32,![]() ≈46.65)
≈46.65)
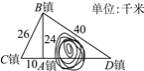
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=-x+4的图象如图所示.
(1)在同一坐标系中,作出一次函数y=2x-5的图象;
(2)用作图象的方法解方程组![]()
(3)求一次函数y=-x+4与y=2x-5的图象与x轴所围成的三角形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边△ABC中,点D,E分别是BC,AC边上的中点,点P为AB边上的一个动点,设AP=x,连接PE,PD,PC,DE,其中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是( )
A.线段PE
B.线段PD
C.线段PC
D.线段DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小慧两位同学在数学活动课中,把长为30cm,宽为10cm的长方形白纸条粘合起来,小明按如图甲所示的方法粘合起来得到长方形ABCD,粘合部分的长度为6cm,小慧按如图乙所示的方法粘合起来得到长方形A1B1C1D1,黏合部分的长度为4cm.
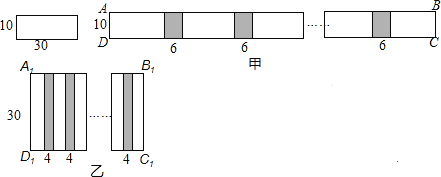
(1)若按小明或小慧的两种方法各粘贴n张,所得的长方形长AB为______,A1B1为______(用含n的代数式表示)
(2)若长为30cm,宽为10cm的长方形白纸条共有100张,求小明应分配到多少张长方形白纸条,才能使小明和小慧按各自要求黏合起来的长方形面积相等(要求100张长方形白纸条全部用完).
查看答案和解析>>
科目:初中数学 来源: 题型:
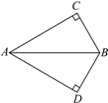
【题目】如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要添加的条件是________或________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织甲、乙两队开展“保护生态环境知识竞赛”,满分为10分,得分均为整数,规定得分达到6分及以上为合格,达到9分及以上为优秀,如图是甲、乙两队学生这次竞赛成绩分布条形统计图.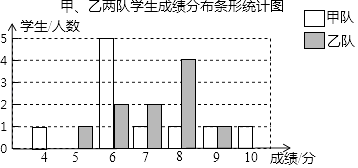
根据以上信息,请解答下面的问题:
(1)在下面甲、乙两队的成绩统计表中,a= , b=c= .
平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
甲队 | a | 6 | c | 2.76 | 90% | 20% |
乙队 | 7.2 | b | 8 | 1.36 | 80% | 10% |
(2)小华同学说:“我在这次比赛中得到了7分,这在我所在的小队成绩中属于中等偏上的位置!”观察(1)中的表格,小华是队的学生;(填“甲”或“乙”)
(3)甲队同学认为:甲队的合格率、优秀率均高于乙队,所以甲队的成绩好于乙队.但乙队同学不同意甲队同学的说法,认为乙队的成绩要好于甲队.请你写出两条支持乙队同学观点的理由.
(4)学校要从从甲、乙两队获得优秀的学生中,选取两名同学参加市级比赛,则恰好同时选中的两人均为甲队学生的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,E分别在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
证明:∵∠1=∠2(已知),∠2=∠3(______)
∴∠1=∠3(______)
∴BD∥CE(______)
∴∠C=∠ABD(______)
又∵∠C=∠D(已知)
∴∠D=∠ABD(_______)
∴________(________)
∴∠A=∠F(________).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com