
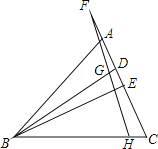
【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C,其中正确的结论有______.
【答案】①②④
【解析】
①根据BD⊥FD,FH⊥BE和∠FGD=∠BGH,证明结论正确;
②根据角平分线的定义和三角形外角的性质证明结论正确;
③证明∠DBE=∠BAC-∠C-∠DBE,根据①的结论,证明结论错误;
④根据角平分线的定义和三角形外角的性质证明结论正确.
解:①∵BD⊥FD,
∴∠FGD+∠F=90°,
∵FH⊥BE,
∴∠BGH+∠DBE=90°,
∵∠FGD=∠BGH,
∴∠DBE=∠F,
①正确;
②∵BE平分∠ABC,
∴∠ABE=∠CBE,
∠BEF=∠CBE+∠C,
∴2∠BEF=∠ABC+2∠C,
∠BAF=∠ABC+∠C,
∴2∠BEF=∠BAF+∠C,
②正确;
③∠ABD=90°-∠BAC,
∠DBE=∠ABE-∠ABD=∠ABE-90°+∠BAC=∠CBD-∠DBE-90°+∠BAC,
∵∠CBD=90°-∠C,
∴∠DBE=∠BAC-∠C-∠DBE,
由①得,∠DBE=∠F,
∴∠F=∠BAC-∠C-∠DBE,
③错误;
④∵∠AEB=∠EBC+∠C,
∵∠ABE=∠CBE,
∴∠AEB=∠ABE+∠C,
∵BD⊥FC,FH⊥BE,
∴∠FGD=∠FEB,
∴∠BGH=∠ABE+∠C,
④正确,
故答案为:①②④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,E分别在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
证明:∵∠1=∠2(已知),∠2=∠3(______)
∴∠1=∠3(______)
∴BD∥CE(______)
∴∠C=∠ABD(______)
又∵∠C=∠D(已知)
∴∠D=∠ABD(_______)
∴________(________)
∴∠A=∠F(________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】胜利中学在一次健康知识竞赛活动中,抽取了一部分学生的测试成绩(成绩均为整数),整理后绘制成如图所示的频数直方图,根据图示信息,下列描述不正确的是( )
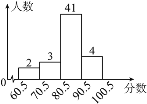
A. 抽查了50名学生
B. 成绩在60.5~70.5分范围的频数为2
C. 成绩在70.5~80.5分范围的频数比成绩在60.5~70.5分范围的频数多1
D. 成绩在70.5~80.5分范围的频率为0.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分5分)画图并填空:
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.
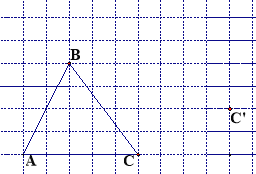
(1)画出平移后的△A′B′C′,(利用网格点和三角板画图)
(2)画出AB边上的高线CD;
(3)画出BC边上的中线AE;
(4)在平移过程中高CD扫过的面积为 .(网格中,每一小格单位长度为1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某电信部门计划修建一条连接B,C两地的电缆.测量人员在山脚A点测得B,C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)?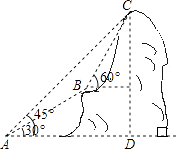
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=12cm,BC=8cm,点E是CD的中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,那么当x=_______时,△APE的面积等于16.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AC=6,线段BC=15,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
解:∵M是AC的中点,AC=6,
∴MC=![]() ______(填线段名称)=______,
______(填线段名称)=______,
又因为CN:NB=1:2,BC=15,
∴CN=![]() ______(填线段名称)=______.
______(填线段名称)=______.
∴MN=______(填线段名称)+______(填线段名称)=8
∴MN的长为8.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com