
【题目】在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1 , 旋转角为θ(0°<θ<90°),连接AC1、BD1 , AC1与BD1交于点P.
(1)如图1,若四边形ABCD是正方形.请直接写出AC1 与BD1的数量关系和位置关系.
(2)如图2,若四边形ABCD是菱形,AC=6,BD=8,判断AC1与BD1的数量关系和位置关系,并给出证明;
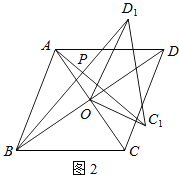
(3)如图3,若四边形ABCD是平行四边形,AC=6,BD=12,连接DD1 , 设AC1=kBD1 , 请直接写出k的值和AC12+(kDD1)2的值.
【答案】
(1)解:AC1=BD1,AC1⊥BD1;
理由:如图1,
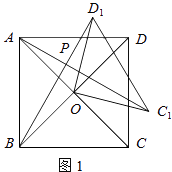
∵四边形ABCD是正方形,
∴OC=OA=OD=OB,AC⊥BD,
∴∠AOB=∠COD=90°,
∵△COD绕点O按逆时针方向旋转得到△C1OD1,
∴OC1=OC,OD1=OD,∠COC1=∠DOD1,
∴OC1=OD1,∠AOC1=∠BOD1=90°+∠AOD1,
在△AOC1和△BOD1中 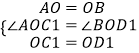 ,
,
∴△AOC1≌△BOD1(SAS);
∴AC1=BD1,
∵∠AOB=90°,∴∠OAB+∠ABP+∠OBD1=90°,
∴∠OAB+∠ABP+∠OAC1=90°,∴∠APB=90°,则AC1⊥BD1;
故AC1 与BD1的数量关系是:AC1=BD1;AC1 与BD1的位置关系是:AC1⊥BD1
(2)解:AC1= ![]() BD1,AC1⊥BD1.
BD1,AC1⊥BD1.
理由:∵四边形ABCD是菱形,
∴OC=OA= ![]() AC,OD=OB=
AC,OD=OB= ![]() BD,AC⊥BD.
BD,AC⊥BD.
∵△C1OD1由△COD绕点O旋转得到,
∴O C1=OC,O D1=OD,∠CO C1=∠DO D1.
∴O C1=OA,O D1=OB,∠AO C1=∠BO D1,
∴ ![]() =
= ![]() .
.
∴ ![]() =
= ![]() .
.
∴△AO C1∽△BOD1.
∴∠O AC1=∠OB D1.
又∵∠AOB=90°,
∴∠O AB+∠ABP+∠OB D1=90°.
∴∠O AB+∠ABP+∠O AC1=90°.
∴∠APB=90°.
∴AC1⊥BD1.
∵△AO C1∽△BOD1,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
即AC1= ![]() BD1,AC1⊥BD1
BD1,AC1⊥BD1
(3)解:如图3,与(2)一样可证明△AOC1∽△BOD1,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴k= ![]() ;
;
∵△COD绕点O按逆时针方向旋转得到△C1OD1,
∴OD1=OD,
而OD=OB,
∴OD1=OB=OD,
∴△BDD1为直角三角形,
在Rt△BDD1中,
BD12+DD12=BD2=144,
∴(2AC1)2+DD12=144,
∴AC12+(kDD1)2=36.
【解析】(1)由旋转的性质和正方形的性质得出对应边相等,各点旋转角相等可推出全等,再根据全等的性质可得出结论;(2)类比(1)的思路方法,可得相似,由对应边成比例,对应角相等可得结论;(3)类比(2),一样可证明△AOC1∽△BOD1,再由旋转的性质可推出△BDD1为直角三角形,再等量代换可得结论.
【考点精析】本题主要考查了相似三角形的判定与性质和旋转的性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】随着科技进步,无人机的应用越来越广,如图,在某一时刻,无人机上的探测器显示,从无人机A处看一栋楼顶部B点的仰角和看与顶部B在同一铅垂线上高楼的底部c的俯角.
(1)如果上述仰角与俯角分别为30。与60。 , 且该楼的高度为30米,求该时刻无人机的竖直高度CD.
(2)如果上述仰角与俯角分别为α与β,且该楼的高度为m米.求用α、β、m表示该时刻无人机的竖直高度CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织甲、乙两队开展“保护生态环境知识竞赛”,满分为10分,得分均为整数,规定得分达到6分及以上为合格,达到9分及以上为优秀,如图是甲、乙两队学生这次竞赛成绩分布条形统计图.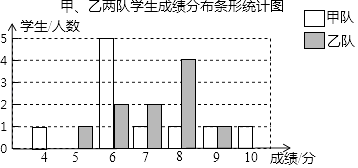
根据以上信息,请解答下面的问题:
(1)在下面甲、乙两队的成绩统计表中,a= , b=c= .
平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
甲队 | a | 6 | c | 2.76 | 90% | 20% |
乙队 | 7.2 | b | 8 | 1.36 | 80% | 10% |
(2)小华同学说:“我在这次比赛中得到了7分,这在我所在的小队成绩中属于中等偏上的位置!”观察(1)中的表格,小华是队的学生;(填“甲”或“乙”)
(3)甲队同学认为:甲队的合格率、优秀率均高于乙队,所以甲队的成绩好于乙队.但乙队同学不同意甲队同学的说法,认为乙队的成绩要好于甲队.请你写出两条支持乙队同学观点的理由.
(4)学校要从从甲、乙两队获得优秀的学生中,选取两名同学参加市级比赛,则恰好同时选中的两人均为甲队学生的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AE=6,CE=2 ![]() ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为开展第二课堂,组织调查了本校300名学生各自最喜爱的一项体育活动,制成了如下扇形统计图,根据统计图判断下列说法,其中正确的一项是( )

A. 在调查的学生中最喜爱篮球的人数是50人
B. 喜欢羽毛球在统计图中所对应的圆心角是144°
C. 其他所占的百分比是20%
D. 喜欢球类运动的占50%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图),然后将剩余部分拼成一个长方形(如图).

(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2-2ab+b2=(a-b)2 B.a2-b2=(a+b)(a-b) C.a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值.
②计算:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )(1-
)(1-![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分5分)画图并填空:
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.
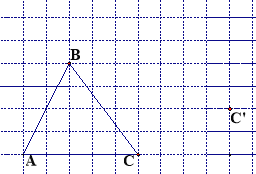
(1)画出平移后的△A′B′C′,(利用网格点和三角板画图)
(2)画出AB边上的高线CD;
(3)画出BC边上的中线AE;
(4)在平移过程中高CD扫过的面积为 .(网格中,每一小格单位长度为1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com