
【题目】在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,P为AC延长线上一点,且∠PBC=![]() ∠BAC,连接DE,BE.
∠BAC,连接DE,BE.
(1)求证:BP是⊙O的切线;
(2)若sin∠PBC=![]() ,AB=10,求BP的长.
,AB=10,求BP的长.
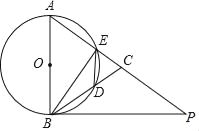
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接AD,求出∠PBC=∠ABC,求出∠ABP=90°,根据切线的判定得出即可;
(2)解直角三角形求出BD,求出BC,根据勾股定理求出AD,根据相似三角形的判定和性质求出BE,根据相似三角形的性质和判定求出BP即可.
(1)连接AD,
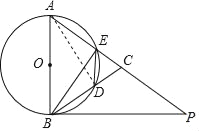
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴AD平分∠BAC,
∴∠BAD=![]() ∠BAC,
∠BAC,
∵∠ADB=90°,
∴∠BAD+∠ABD=90°,
∵∠PBC=![]() ∠BAC,
∠BAC,
∴∠PBC+∠ABD=90°,
∴∠ABP=90°,即AB⊥BP,
∴PB是⊙O的切线;
(2)∵∠PBC=∠BAD,
∴sin∠PBC=sin∠BAD,
∵sin∠PBC=![]() =
=![]() ,AB=10,
,AB=10,
∴BD=2![]() ,由勾股定理得:AD=
,由勾股定理得:AD=![]() =4
=4![]() ,
,
∴BC=2BD=4![]() ,
,
∵由三角形面积公式得:AD×BC=BE×AC,
∴4![]() ×4
×4![]() =BE×10,
=BE×10,
∴BE=8,
∴在Rt△ABE中,由勾股定理得:AE=6,
∵∠BAE=∠BAP,∠AEB=∠ABP=90°,
∴△ABE∽△APB,
∴![]() =
=![]() ,
,
∴PB=![]() =
=![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴的交点为
轴的交点为![]() ,顶点部分为
,顶点部分为![]() ,若点
,若点![]() 是四边形
是四边形![]() 边上的点,则
边上的点,则![]() 的最大值为( )
的最大值为( )
A. -6 B. -8 C. -12 D. -18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为18,BP=4,则AB的长为_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(3)班数学兴趣小组经过市场调查,整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天的销 售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x之间的函数表达式;
(2)销售该商品在第几天时,当天获得的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.

(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com