
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
【答案】解:(1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,又BF⊥CE,
∴∠CBG+∠BCF=90°,又∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
∴△AEC≌△CGB,
∴AE=CG,
(2)BE=CM,
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵AC=BC,∠ACM=∠CBE=45°,
∴△BCE≌△CAM,
∴BE=CM.
【解析】
⑴证明:设∠ACE=∠1,因为直线BF垂直于CE,交CE于点F,所以∠CFB=90°,
所以∠ECB+∠CBF=90°.
又因为∠1+∠ECB=90°,所以∠1=∠CBF .
因为AC="BC," ∠ACB=90°,所以∠A=∠CBA=45°.
又因为点D是AB的中点,所以∠DCB=45°.
因为∠1=∠CBF,∠DCB=∠A,AC=BC,所以△CAE≌△BCG,所以AE=CG.
(2)解:CM=BE.证明如下:因为∠ACB=90°,所以∠ACH +∠BCF=90°.
因为 CH⊥AM,即∠CHA=90°,所以 ∠ACH +∠CAH=90°,所以∠BCF=∠CAH.
因为 CD为等腰直角三角形斜边上的中线,所以 CD=AD.所以∠ACD=45°.
在△CAM与△BCE中,CA=BC,∠CAH =∠BCF, ∠ACM =∠CBE,
所以 △CAM ≌△BCE,所以CM=BE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某区对参加2019年中考的300名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图.

请根据图表信息回答下列问题:
(1)![]() __________,
__________,![]() __________;
__________;
(2)将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均为正常,据以上信息估计全区初中毕业生中视力正常的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点G为位似中心的位似图形,它们的顶点都在小正方形顶点上.
(1)画出位似中心点G;
(2)若点A、B在平面直角坐标系中的坐标分别为(﹣6,0),(-3,2),点P(m,n)是线段AC上任意一点,则点P在△A′B′C′上的对应点P′的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线EF分别与直线AB,CD相交于点F,E,EM平分∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点。
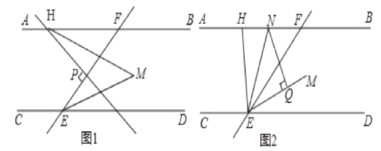
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数。
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在反比例函数y=![]() 的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
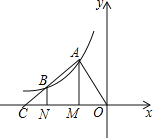
A.2 B.4 C.﹣2 D.﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=9,N为AB上一点,且AN=3,BC的高线AD交BC于点D,M是AD上的动点,连结BM,MN,则BM+MN的最小值是 ( )
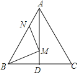
A. ![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com