
【题目】已知:直线EF分别与直线AB,CD相交于点F,E,EM平分∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点。
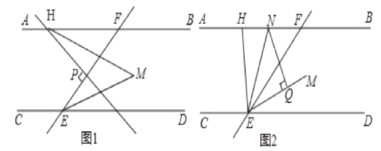
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数。
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论。
【答案】(1)45o (2)∠FHE=2∠ENQ或∠FHE=180°2∠ENQ,证明见解析
【解析】
(1)首先作MQ∥AB,根据平行线的性质,推得∠M=![]() (∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.
(∠FHP+∠HFP);然后根据HP⊥EF,推得∠FHP+∠HFP=90°,据此求出∠M的度数即可.
(2)①如图2,首先判断出∠NEQ=∠NEF+∠QEF=![]() (∠HEF+∠DEF)=
(∠HEF+∠DEF)=![]() ∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=
∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=![]() (180°-∠HED)=
(180°-∠HED)=![]() ∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.
∠CEH,再根据AB∥CD,推得∠FHE=2∠ENQ即可.
②如图3,首先判断出∠NEQ=∠QEF-∠NEF=![]() (∠DEF-∠HEF)=
(∠DEF-∠HEF)=![]() ∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=
∠HED,然后根据NQ⊥EM,可得∠NEQ+∠ENQ=90°,推得∠ENQ=![]() (180°-∠HED)=
(180°-∠HED)=![]() ∠CEH,再根据AB∥CD,推得∠FHE=180°-2∠ENQ即可.
∠CEH,再根据AB∥CD,推得∠FHE=180°-2∠ENQ即可.
如图1,作MQ∥AB,
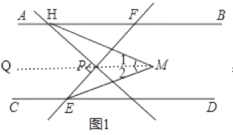
∵AB∥CD,MQ∥AB,
∴MQ∥CD,
∴∠1=∠FHM,∠2=∠DEM,
∴∠1+∠2=∠FHM+∠DEM=![]() (∠FHP+∠FED)=
(∠FHP+∠FED)= ![]() (∠FHP+∠HFP),
(∠FHP+∠HFP),
∵HP⊥EF,
∴∠HPF=90°,
∴∠FHP+∠HFP=180°90°=90°,
∵∠1+∠2=∠M,
∴∠M=![]() ×90°=45°.
×90°=45°.
(2)①如图2,
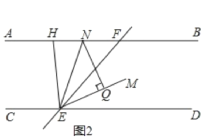
∠FHE=2∠ENQ,理由如下:
∠NEQ=∠NEF+∠QEF=![]() (∠HEF+∠DEF)=
(∠HEF+∠DEF)= ![]() ∠HED,
∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=![]() (180°∠HED)=
(180°∠HED)= ![]() ∠CEH,
∠CEH,
∵AB∥CD,
∴∠FHE=∠CEH=2∠ENQ.
②如图3,
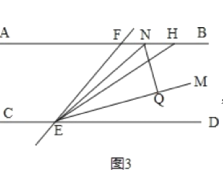
∠FHE=180°2∠ENQ,理由如下:
∠NEQ=∠QEF∠NEF=![]() (∠DEF∠HEF)=
(∠DEF∠HEF)= ![]() ∠HED,
∠HED,
∵NQ⊥EM,
∴∠NEQ+∠ENQ=90°,
∴∠ENQ=![]() (180°∠HED)=
(180°∠HED)= ![]() ∠CEH,
∠CEH,
∵AB∥CD,
∴∠FHE=180°∠CEH=180°2∠ENQ.
综上,可得当H在直线AB上运动(不与点F重合)时,∠FHE=2∠ENQ或∠FHE=180°2∠ENQ.


科目:初中数学 来源: 题型:
【题目】如图(1)是用硬纸板做成的两个全等的直角三角形,两直角边的长分别为![]() 和
和![]() 斜边长为
斜边长为![]() 图(2)是以
图(2)是以![]() 为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个直角梯形.
为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个直角梯形.
(1)在图(3)处画出拼成的这个图形的示意图;
(2)利用(1)画出的图形证明勾股定理.
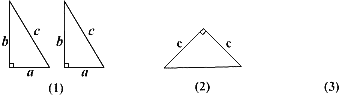
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.

(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的直径为10,点A、点B、点C在⊙O上,∠CAB的平分线交⊙O于点D.


(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD的长;
(2)如图②,若∠CAB=60°,CF⊥BD,①求证:CF是⊙O的切线;②求由弦CD、CB以及弧DB围成图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.



(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴,并在所给坐标系中画出该函数的图象;
(3)该函数的图象经过怎样的平移得到y=x2的图象?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距离O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,
(1)A处是否会受到火车的影响,并写出理由
(2)如果A处受噪音影响,求影响的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,交y轴于C点,其中B点坐标为(3,0),C点坐标为(0,3),且图象对称轴为直线x=1.
(1)求此二次函数的关系式;
(2)P为二次函数y=ax2+bx+c图象上一点,且S△ABP=S△ABC,求P点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com