
【题目】已知二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴,并在所给坐标系中画出该函数的图象;
(3)该函数的图象经过怎样的平移得到y=x2的图象?

【答案】(1)b=-4,c=3;(2)顶点坐标为(2,﹣1),对称轴是直线x=2,图象见解析;(3)将该函数的图象向左平移2个单位,再向上平移1个单位得到y=x2的图象.
【解析】试题分析:(1)根据题意,将点(4,3),(3,0)分别代入二次函数解析式中,得二元一次方程组求解即可。
(2)由(1)可得二次函数解析式,将二次函数解析式化为顶点式即可。
(3)根据二次函数的顶点、对称轴、以及所过的点画出图象即可。
解:(1)将(4,3),(3,0)代入y=x2+bx+c,得![]() ,解得:
,解得:![]() ,
,
(2)二次函数y=x2﹣4x+3=(x﹣2)2﹣1,
则顶点坐标为(2,﹣1),对称轴是直线x=2,
如图,
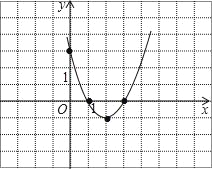
(3)将该函数的图象向左平移2个单位,再向上平移1个单位得到y=x2的图象.
点睛:本题是二次函数综合题,熟练掌握待定系数法求二次函数的解析式,二次函数一般式与顶点式的转化,二次函数的图像变化是解答本题的关键.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴ (同角的补角相等)①
∴ (内错角相等,两直线平行)②
∴∠ADE=∠3( )③
∵∠3=∠B( )④
∴ (等量代换)⑤
∴DE∥BC( )⑥
∴∠AED=∠C( )⑦

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个转盘被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;(③指针指向黄色;④指针不指向黄色,估计各事件的可能性大小,完成下列问题.
(1)④事件发生的可能性大小是 ;
(2)多次实验,指针指向绿色的频率的估计值是 ;
(3)将这些事件的序号按发生的可能性从小到大的顺序排列为: ![]()
![]()
![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售一种成本价为每件60元的商品,规定销售期间销售单价不低于成本价,且每件获利不得高于成本价的45%.经测算,每天的销售量y(件)与销售单价x(元)的关系符合一次函数y=﹣x+120,设该网店每天销售该商品所获利润为W(元).
(1)试写出利润W与销售单价x之间的函数关系式;
(2)销售单价定为多少元时,该网店每天销售该商品可获得最大利润,最大利润是多少元?
(3)若该网店每天销售该商品所获利润不低于500元,请直接写出销售单价x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线EF分别与直线AB,CD相交于点F,E,EM平分∠FED,AB∥CD,H,P分别为直线AB和线段EF上的点。
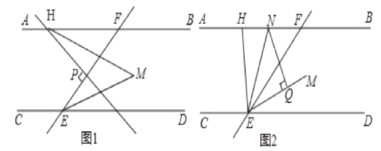
(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数。
(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张桌子可坐6人,按下列方式将桌子拼在一起.

①2张桌子拼在一起可坐_____人,4张桌子拼在一起可坐_______人,![]() 张桌子拼在一起可坐(_____________)人.
张桌子拼在一起可坐(_____________)人.
②一家餐厅有40张这样的长方形桌子,按照上图方式每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐__________人.
③若在②中,改成8张桌子拼成一张大桌子,则共可坐________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请在图中作出△A′B′C′;(2)写出点A′、B′、C′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图像与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为(-1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>3.其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com