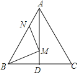
【题目】如图，在等边△ABC中，AB＝9，N为AB上一点，且AN＝3，BC的高线AD交BC于点D，M是AD上的动点，连结BM，MN，则BM+MN的最小值是 （ ）
A. 
B. 
C. 
D. 4
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】已知：在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．
（1）直线BF垂直于直线CE于点F，交CD于点G（如图1），求证：AE=CG；
（2）直线AH垂直于直线CE，垂足为点H，交CD的延长线于点M（如图2），找出图中与BE相等的线段，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
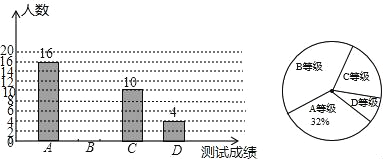
【题目】某中学为了了解九年级学生体能状况，从九年级学生中随机抽取部分学生进行体能测试，测试结果分为A，B，C，D四个等级，并依据测试成绩绘制了如下两幅尚不完整的统计图；
（1）这次抽样调查的样本容量是 ，并补全条形图；
（2）D等级学生人数占被调查人数的百分比为 ，在扇形统计图中C等级所对应的圆心角为 °；
（3）该校九年级学生有1500人，请你估计其中A等级的学生人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，交y轴于C点，其中B点坐标为（3，0），C点坐标为（0，3），且图象对称轴为直线x=1．
（1）求此二次函数的关系式；
（2）P为二次函数y=ax2+bx+c图象上一点，且S△ABP=S△ABC，求P点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一段抛物线：y=﹣x（x﹣2）（0≤x≤2）记为C1，它与x轴交于两点O，A1；将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3；…如此进行下去，得到Cn，若点P（2017，m）在抛物线Cn上，则m为（ ）
A. 1 B. ﹣1 C. 2 D. ﹣2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市正在创建“全国文明城市”，光明学校拟举办“创文知识”抢答案，欲购买
两种奖品以抢答者.如果购买
种25件，
种20件，共需480元；如果购买种15件，种25件，共需340元.
（1）两种奖品每件各多少元？
（2）现要购买两种奖品共100件，总费用不超过1120元，那么最多能购买种奖品多少件？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在
中，
，点
在
上，连接
，
.
（1）如图1，求证：
；
（2）如图2，点
为的中点，过点作的垂线分别交的延长线，
的延长线，
于点
，求证：
；
（3）如图3，在（2）的条件下，过点分别作
于点
于点
，若
，
，求
的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD的对角线交于点O，点E是矩形外一点，
，
，
，连接AE交BD于点F、连接CF．
求证：四边形BECO是菱形；
填空：若
，则线段CF的长为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y=-2x+4与x轴y轴相交于A，B两点，点C在线段AB上，且∠COA=45°．
(1)求点A，B的坐标；
(2)求△AOC的面积；
(3)直线OC上有一动点D，过点D作直线l(不与直线AB重合)与x，y轴分别交于点E，F，当△OEF与△ABO全等时，求直线EF的解析式．
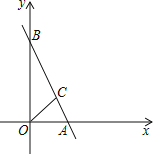
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
