
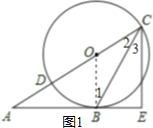
【题目】(12分)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.

(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
【答案】
【解析】试题分析:(1)证明:如图1,连接OB,由AB是⊙0的切线,得到OB⊥AB,由于CE丄AB,的OB∥CE,于是得到∠1=∠3,根据等腰三角形的性质得到∠1=∠2,通过等量代换得到结果.
(2)如图2,连接BD通过△DBC∽△CBE,得到比例式![]() ,列方程可得结果.
,列方程可得结果.
(1)证明:如图1,连接OB,
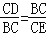
∵AB是⊙0的切线,
∴OB⊥AB,
∵CE丄AB,
∴OB∥CE,
∴∠1=∠3,
∵OB=OC,
∴∠1=∠2,
∴∠2=∠3,
∴CB平分∠ACE;
(2)如图2,连接BD,
∵CE丄AB,
∴∠E=90°,
∴BC=![]() =
=![]() =5,
=5,
∵CD是⊙O的直径,
∴∠DBC=90°,
∴∠E=∠DBC,
∴△DBC∽△CBE,
∴![]() ,
,
∴BC2=CDCE,
∴CD=![]() =
=![]() ,
,
∴OC=![]() =
=![]() ,
,
∴⊙O的半径=![]() .
.


科目:初中数学 来源: 题型:
【题目】为丰富学生的课余生活,陶冶学生的情操,促进学生全面发展,某中学七年级开展了学生社团活动,学校为了解学生参加情况,对部分学生进行了调查,制作出如下的统计图:

请根据统计图,完成以下问题:
(1)这次共调查了 名学生;在扇形统计图中,表示“书法类”所在扇形的圆心角是 度.
(2)请把统计图1 补充完整.
(3)若七年级共有学生1100 名,请估算有多少名学生参加文学类社团.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
①3x2﹣[2x2y﹣(xy﹣x2)]+4x2y
②![]() ×
×![]()
③|﹣3|+(﹣1)2013×(π﹣3)0﹣
④[(3a+b)2﹣(2a﹣b)(﹣b﹣2a)]÷a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() ,作射线
,作射线![]() ,再分别作上
,再分别作上![]() 和
和![]() 的平分线
的平分线![]() 、
、![]() .
.
(1) 如图①,当![]() 时,求
时,求![]() 的度数;
的度数;
(2) 如图②,当射线![]() 在
在![]() 内绕
内绕![]() 点旋转时,
点旋转时,![]() 的大小是否发生变化,说明理由.
的大小是否发生变化,说明理由.
(3) 当射线![]() 在
在![]() 外绕
外绕![]() 点旋转且
点旋转且![]() 为钝角时,画出图形,请直接写出相应的
为钝角时,画出图形,请直接写出相应的![]() 的度数(不必写出过程) .
的度数(不必写出过程) .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天) | 豪华间(元/人/天) | 贵宾间(元/人/天) | |
三人间 | 50 | 100 | 500 |
双人间 | 70 | 150 | 800 |
单人间 | 100 | 200 | 1500 |
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB,请按要求完成下列问题.
(1)用直尺和圆规作图,延长线段AB到点C,使BC=AB;反向延长线段AB到点D,使AD=AC;
(2)如果AB=2cm;①求CD的长度;②设点P是线段BD的中点,求线段CP的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A(3,0),B两点,与y轴交于点C,点M(
与x轴交于A(3,0),B两点,与y轴交于点C,点M(![]() ,5)是抛物线
,5)是抛物线![]() 上一点,抛物线
上一点,抛物线![]() 与抛物线
与抛物线![]() 关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′
关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′
(1)求抛物线C1的解析式;
(2)过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D. P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com